The Project Gutenberg EBook of Einstein et l'univers, by Charles Nordmann

This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever.  You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org


Title: Einstein et l'univers
       Une lueur dans le mystère des choses

Author: Charles Nordmann

Release Date: January 23, 2013 [EBook #41903]

Language: French

Character set encoding: ISO-8859-1

*** START OF THIS PROJECT GUTENBERG EBOOK EINSTEIN ET L'UNIVERS ***




Produced by Claudine Corbasson, Hans Pieterse and the
Online Distributed Proofreading Team at http://www.pgdp.net
(This file was produced from images generously made
available by The Internet Archive/Canadian Libraries)

EINSTEIN
ET
L'UNIVERS

• LE ROMAN DE LA SCIENCE •

CHARLES NORDMANN

Astronome de l'Observatoire de Paris

EINSTEIN
ET
L'UNIVERS

UNE LUEUR DANS
LE MYSTÈRE DES CHOSES

LIBRAIRIE HACHETTE

Tous droits de traduction, de reproduction
et d'adaptation réservés pour tous pays,
Copyright par Librairie Hachette, 1921.

Dans ce mur qui nous masque la réalité un coup gigantesque vient d'être porté par un homme supérieur, Einstein. Grâce à lui, à travers la brèche entr'ouverte, un peu des lumières cachées filtre maintenant jusqu'à nous, et le regard en est charmé, ébloui.

Je voudrais glisser dans ce livre, avec des mots simples et clairs si je puis, un léger reflet de cet éblouissement.

Les théories d'Einstein causent dans la Science un profond bouleversement. Grâce à elles le monde nous paraîtra plus simple, plus coordonné, plus uni. Nous [6] sentirons mieux désormais qu'il est grandiose, cohérent, réglé par une harmonie inflexible. Un peu de l'ineffable nous deviendra plus clair.

Les hommes traversent l'Univers, pareils à ces poussières qui, dans l'or fin du rayon de soleil filtrant par une persienne, dansent un instant puis retombent aux ténèbres. Est-il une manière plus belle et plus noble de remplir la vie que de se gorger les yeux, la tête et le cœur de l'immortel et pourtant si fugitif rayon? Regarder, chercher à comprendre le magnifique et surprenant spectacle de l'Univers, quelle plus haute volupté?

Dans la réalité il y a plus de merveilleux, de romanesque que dans toutes nos pauvres rêveries. Dans la soif de savoir, dans l'élan mystique qui nous jette au cœur profond de l'Inconnu, il y a plus de passion et de douceur que dans toutes les fadaises dont s'alimentent tant de littératures. C'est pourquoi j'ai peut-être tort, après tout, de dire que ce livre n'est pas un roman.

Je tâcherai d'y faire comprendre, avec exactitude et pourtant sans l'appareil ésotérique des techniciens, la révolution apportée par Einstein. Je tâcherai aussi d'en marquer les limites et de préciser ce que, au total, nous pouvons réellement connaître aujourd'hui du monde extérieur vu à travers l'écran translucide de la Science.

Il n'est point de Révolution que bientôt ne suive une réaction, suivant ce rythme sinusoïdal qui semble la démarche éternelle de l'esprit humain. Einstein est à la [7] fois le Sieyès, le Mirabeau et le Danton de la Révolution nouvelle. Mais celle-ci déjà connaît des Marat fanatiques et qui prétendent dire à la Science: «Tu n'iras pas plus loin.»

C'est pourquoi une opposition se dessine contre les prétentions d'apôtres trop zélés du nouvel évangile scientifique. A l'Académie des Sciences, M. Paul Painlevé, avec la force d'un génie mathématique rigoureux, vient de se dresser entre Newton qu'on croyait écrasé et Einstein.

J'examinerai dans mes conclusions la pénétrante critique du géomètre français. Elle m'aidera à situer exactement, dans l'évolution de nos idées, la splendide synthèse einsteinienne que je veux d'abord exposer avec tout l'amour qu'il faut vouer aux choses pour les bien comprendre.

Avec Einstein la Science n'a point achevé sa tâche. Il laisse encore plus d'un «gouffre interdit à nos sondes» et où demain quelque autre esprit supérieur projettera sa clarté.

Ce qui fait l'adorable et hautaine grandeur de la Science, c'est qu'elle est un perpétuel devenir. Dans la sombre forêt du Mystère, la Science est comme une clairière; l'homme élargit sans cesse le cercle qui la borde; mais en même temps et par cela même, il se trouve en contact sur un plus grand nombre de points à la fois avec les ténèbres de l'Inconnu. Dans cette forêt [8] peu d'hommes ont porté la hache étincelante aussi loin qu'Einstein.

En dépit des basses préoccupations qui, de toutes parts, nous harcèlent, parmi tant de misérables contingences, le système d'Einstein apparaît plein de grandeur.

L'actualité est comme cette mousse bruissante et légère qui couronne et masque un instant l'or du vin généreux. Quand tout le bruit fugace qui emplit aujourd'hui nos oreilles sera éteint, la théorie d'Einstein se dressera comme le phare essentiel au seuil de ce triste et petit vingtième siècle.

Charles Nordmann.

Mais, tandis que, pour accéder à Spinoza, il n'est que d'entendre un peu de latin, des monstres effrayants montent la garde devant Einstein et s'efforcent par des grimaces horribles d'en défendre l'approche.

Ils s'agitent derrière d'étranges grilles mouvantes, tantôt rectangulaires et tantôt curvilignes qu'on appelle des «coordonnées».

Ils portent des noms monstrueux comme eux-mêmes. [10] Ils s'appellent vecteurs contrevariants et covariants, tenseurs, scalaires, déterminants, vecteurs orthogonaux, symboles à trois indices généralisés, que sais-je....

Tous ces êtres, importés du fond le plus sauvage de la jungle mathématique, s'accolent ou se subdivisent dans une promiscuité étrange, par ces chirurgies étonnantes qu'on appelle l'intégration et la différentiation.

Bref si Einstein est un trésor, un horrible troupeau de reptiles mathématiques en éloigne le curieux. Qu'il y ait en eux, comme dans les gargouilles gothiques, une secrète beauté, c'est certain.

Mais il vaut mieux, armés du fouet éclatant qu'est le verbe, les chasser loin de nous et monter jusqu'aux splendeurs einsteiniennes par le clair et noble escalier du langage français.

Qui est le physicien Einstein? Il n'importe point ici. Sachons seulement qu'il a refusé de signer naguère l'immonde manifeste des 93, ce qui lui a valu les persécutions des pangermanistes.

Au surplus, les vérités géométriques, les découvertes scientifiques ont une valeur intrinsèque qui doit être jugée et pesée objectivement, quel que soit celui qui les a trouvées.

Pythagore eût-il été le dernier des criminels et des malhonnêtes gens, cela n'enlèverait rien à la validité du carré de l'hypoténuse. Un théorème est vrai ou faux, que le nez de son auteur ait la ligne aquiline des fils de Sem, camuse de ceux de Cham ou rectiligne de ceux de Japhet. Est-ce réellement un signe que l'humanité [11] est asymptote à la perfection, que d'entendre dire quelquefois: «Dis-moi quel temple tu fréquentes et je te dirai si ta géométrie est juste»? La Vérité n'a pas besoin d'état-civil. Passons.

Toutes nos notions, toute la science, toute la vie pratique elle-même sont fondées sur la représentation que nous nous faisons des aspects successifs des choses. Notre esprit, aidé par nos sens, classe avant tout celles-ci dans le temps et dans l'espace, qui sont les deux cadres où nous fixons d'abord ce qui nous est sensible dans le monde extérieur. Écrivons-nous une lettre: nous mettons en suscription le lieu et la date. Ouvrons-nous un journal: ce sont ces indications qui y précèdent toutes les dépêches. Il en est de même en tout et pour tout. Le temps et l'espace, la situation des choses et leur époque apparaissent ainsi comme les piliers jumeaux de toute connaissance, les deux colonnes sur lesquelles repose l'édifice de l'entendement humain.

Leconte de Lisle l'a bien senti, lorsque avec sa profonde et philosophique intelligence il écrivait, s'adressant pathétiquement à la divine mort:

Le nombre n'est ici que pour définir quantitativement le temps et l'espace, et Leconte de Lisle a bien exprimé, [12] dans ces vers magnifiques et célèbres, que ce qui existe pour nous dans le vaste monde, ce que nous y savons, voyons, tout l'ineffable et trouble écoulement des phénomènes ne nous présente un aspect défini, une forme précise qu'après avoir traversé ces deux filtres superposés que notre entendement interpose: le temps et l'espace.

Ce qui donne aux travaux d'Einstein leur importance, c'est qu'il a montré, comme nous allons voir, que l'idée que nous nous faisions du temps et de l'espace doit être complètement revisée. Si cela est, la science tout entière,—et avec elle la psychologie,—doit être refondue. Telle est la première partie de l'œuvre d'Einstein. Mais là ne s'est pas bornée l'action de son profond génie. Si elle n'était que cela, elle n'eût été que négative.

Après avoir démoli, après avoir déblayé nos connaissances de ce qu'on croyait en être le piédestal inébranlable et qui n'était, selon lui, qu'un échafaudage fragile masquant les harmonieuses proportions de l'édifice, il a reconstruit. Il a creusé dans le monument de vastes fenêtres qui permettent maintenant de jeter un regard émerveillé sur les trésors qu'il recèle. En un mot, Einstein a d'une part montré, avec une acuité et une profondeur étonnantes, que la base de nos connaissances semble n'être pas ce qu'on a cru et doit être refaite avec un nouveau ciment. D'autre part, il a, sur cette base, renouvelé, rebâti l'édifice démoli dans ses fondements mêmes, et lui a donné une forme hardie dont la beauté et l'unité sont grandioses.

Il me reste maintenant à tâcher de préciser, d'une [13] manière concrète et aussi exacte que possible, ces généralités. Mais je dois insister d'abord sur un point qui a une signification considérable: si Einstein s'était borné à la première partie de son œuvre,—telle que je viens de l'esquisser,—celle qui ébranle les notions classiques de temps et d'espace, il n'aurait point, dans le monde de la pensée, la gloire qui, dès aujourd'hui, auréole son nom.

La chose est d'importance, car la plupart de ceux qui,—en dehors des spécialistes purs,—ont écrit sur Einstein, ont insisté surtout, et souvent exclusivement, sur ce côté en quelque sorte «démolisseur» de son intervention. Or, on va voir qu'à ce point de vue, Einstein n'a pas été le premier ni le seul. Il n'a fait qu'aiguiser davantage et enfoncer un peu plus, entre les blocs mal joints de la science classique, le burin que d'autres avant lui, et surtout le grand Henri Poincaré, y avaient dès longtemps porté. Ensuite il me restera à expliquer, si je puis, le grand, l'immortel titre d'Einstein à la reconnaissance des hommes, qui est, sur cette œuvre critique, d'avoir reconstruit, réédifié par ses propres forces quelque chose de magnifique et de neuf: et ici, sa gloire est sans partage.

La science entière depuis Aristote jusqu'aujourd'hui a été fondée sur l'hypothèse ou, pour mieux dire, sur les hypothèses qu'il existe un temps absolu et un espace [14] absolu. Autrement dit, on a fait reposer nos notions sur l'idée qu'un intervalle de temps et un intervalle spatial entre deux phénomènes donnés sont toujours les mêmes, pour quelque observateur que ce soit, et quelles que soient les conditions d'observation. Par exemple, il ne fût venu à l'esprit de personne, tant que régna la science classique, que l'intervalle de temps, le nombre de secondes qui sépare deux éclipses successives de soleil, pût ne pas être un nombre fixe et identiquement le même pour un observateur placé sur la terre et un observateur placé sur Sirius (la seconde étant d'ailleurs définie pour tous deux par le même chronomètre). De même, personne n'eût imaginé que la distance en mètres de deux objets, par exemple la distance de la Terre au Soleil à un instant donné, mesurée trigonométriquement, pût ne pas être la même pour un observateur placé sur la Terre et un autre placé sur Sirius (le mètre étant d'ailleurs défini pour tous deux par la même règle).

«Il existe, dit Aristote[1], un seul et même temps qui s'écoulera en deux mouvements d'une manière semblable et simultanée; et si ces deux temps n'étaient pas simultanés, ils seraient encore de la même espèce.... Ainsi, pour des mouvements qui s'accomplissent simultanément, il y a un seul et même temps, que ces mouvements soient, ou non, également vites; et cela, lors même que l'un d'eux serait un mouvement local et [15] l'autre une altération.... Par conséquent, les mouvements peuvent être autres et se produire indépendamment l'un de l'autre; de part et d'autre, le temps est absolument le même.» Cette définition aristotélicienne du temps physique date de plus de deux mille ans. Elle représente avec beaucoup de clarté l'idée de temps telle qu'elle a été acceptée jusqu'à ces toutes dernières années par la science classique, en particulier par la mécanique de Galilée et de Newton.

Pourtant il semble qu'en face d'Aristote, Épicure déjà ait esquissé l'attitude qui plus tard opposera Einstein à Newton. Voici en effet ce qu'écrit Lucrèce exposant la doctrine épicurienne:

«Le temps n'existe pas par lui-même, mais par les objets sensibles seuls, dont résulte la notion de passé, de présent, d'avenir. On ne peut concevoir le temps en soi et indépendamment du mouvement ou du repos des choses[2].»

En fait, l'espace ainsi que le temps ont été considérés par la science depuis Aristote comme des données invariables, fixes, rigides, absolues. Newton ne pensait rien dire que d'évident et de banal lorsqu'il écrivait dans son célèbre Scholie: «Le temps absolu, vrai et mathématique pris en soi et sans relation à aucun objet extérieur, coule uniformément par sa propre nature.... L'espace absolu, d'autre part, indépendant par sa propre nature de toute relation à des objets [16] extérieurs, demeure toujours immuable et immobile.»

Toute la science, toute la physique et la mécanique, telles qu'on les enseigne encore aujourd'hui dans les lycées et dans la plupart des universités, sont fondées entièrement sur ces énoncés, sur ces notions d'un temps et d'un espace absolus, pris en soi et sans relation à aucun objet extérieur, indépendants par leur propre nature.

En un mot, et si j'ose employer cette image, le temps de la science classique était semblable à un fleuve portant les phénomènes ainsi que des navires, mais qui ne s'écoule pas moins et d'un même mouvement quand il n'y a pas de navires. Pareillement, l'espace était un peu comme la rive de ce fleuve et insensible aux navires qui passent.

Pourtant, dès l'époque de Newton, dès même celle d'Aristote, un métaphysicien un peu réfléchi aurait pu apercevoir qu'il y avait quelque apparence choquante dans ces définitions.

Le Temps absolu, l'Espace absolu sont de ces «choses en soi» que l'esprit humain a de tout temps considérées comme lui étant directement inaccessibles. Les spécifications d'espace et de temps, ces étiquettes numérotées que nous attachons aux objets du monde extérieur, ainsi qu'on fait dans les gares aux colis pour ne les point perdre (... et la précaution n'est pas toujours suffisante), ces données ne nous sont fournies par nos sens, armés ou non d'instruments, qu'à l'occasion d'impressions concrètes. En aurions-nous la notion [17] en l'absence de corps attachés à ces données, ou plutôt auxquels nous attachons ces données? L'affirmer comme font Aristote, Newton, la science classique, c'est faire une supposition audacieuse, et non nécessairement fondée.

Le seul temps dont nous ayons la notion, en dehors de tout objet, est le temps psychologique si lumineusement scruté par M. Bergson, et qui n'a aucun rapport, que son nom, avec le temps des physiciens, de la science.

C'est en réalité Henri Poincaré, ce grand Français dont la disparition laisse un vide qui ne sera jamais comblé, qui a le mérite d'avoir, avec la plus grande netteté et la plus intelligente hardiesse, soutenu la thèse que le temps et l'espace, tels qu'ils nous sont donnés, ne peuvent être que relatifs.

Quelques textes ici ne seront pas inutiles; ils montreront qu'Henri Poincaré a vraiment le mérite de la plupart des choses qu'on attribue, dans le public, couramment à Einstein. De cette démonstration, le mérite d'Einstein ne sera pas diminué, car il est ailleurs, nous le montrerons.

Voici comment s'exprimait Henri Poincaré, dont l'enveloppe charnelle a péri, il y a des années déjà, mais dont la pensée continue à dominer tous les cerveaux qui réfléchissent, étendant plus loin chaque jour ses ailes triomphales:

«Il est impossible de se représenter l'espace vide.... C'est de là que provient la relativité irréductible de l'espace. Quiconque parle de l'espace absolu emploie [18] un mot vide de sens. Je suis en un point déterminé de Paris, place du Panthéon, par exemple, et je dis: Je reviendrai ici demain. Si on me demande: Entendez-vous que vous reviendrez au même point de l'espace? je serai tenté de répondre: Oui. Et cependant j'aurai tort, puisque d'ici à demain la Terre aura marché, entraînant avec elle la place du Panthéon, qui aura parcouru plus de 2 millions de kilomètres. Et si je voulais préciser mon langage, je n'y gagnerais rien, puisque ces 2 millions de kilomètres, notre globe les a parcourus dans son mouvement par rapport au Soleil, que le Soleil se déplace à son tour par rapport à la Voie Lactée, que La Voie lactée elle-même est sans doute en mouvement sans que nous puissions connaître sa vitesse. De sorte que nous ignorons complètement et que nous ignorerons toujours de combien la place du Panthéon se déplace en un jour. En somme, j'ai voulu dire: Demain, je verrai de nouveau le dôme et le fronton du Panthéon, et s'il n'y avait pas de Panthéon, ma phrase n'aurait aucun sens et l'espace s'évanouirait....»

Poincaré complète ainsi sa pensée:

«Supposons que, dans une nuit, toutes les dimensions de l'Univers deviennent mille fois plus grandes: le monde sera resté semblable à lui-même, en donnant au mot de similitude le même sens qu'au troisième livre de géométrie. Seulement, ce qui avait un mètre de long mesurera désormais un kilomètre, ce qui était long d'un millimètre deviendra long d'un mètre. Ce lit où je suis couché, et mon corps lui-même se seront agrandis [19] dans la même proportion. Quand je me réveillerai le lendemain matin, quel sentiment éprouverai-je en présence d'une aussi étonnante transformation? Eh bien! je ne m'apercevrai de rien du tout. Les mesures les plus précises seront incapables de me rien révéler de cet immense bouleversement, puisque les mètres dont je me servirai auront varié précisément dans les mêmes proportions que les objets que je chercherais à mesurer. En réalité, ce bouleversement n'existe que pour ceux qui raisonnent comme si l'espace était absolu. Si j'ai raisonné un instant comme eux, c'est pour mieux faire voir que leur façon de voir implique contradiction.»

On peut facilement étendre ce raisonnement de Poincaré. Si tous les objets de l'Univers devenaient par exemple mille fois plus hauts, et mille fois moins larges, nous n'aurions non plus aucun moyen de nous en apercevoir, car nous-mêmes et nos rétines et les mètres dont nous nous servirions pour mesurer les objets, serions déformés en même temps et de même. Bien plus, si tous les objets de l'Univers subissaient une déformation spatiale absolument irrégulière, si un génie invisible et tout-puissant le distordait d'une manière quelconque, en tirant sur lui comme sur une masse de caoutchouc, nous n'aurions aucun moyen de le savoir. Rien ne tend mieux à prouver que l'espace est relatif, et que nous ne pouvons concevoir l'espace en dehors des objets qui servent à le mesurer. Pas de mètre, pas d'espace.

Poincaré a poussé si loin ses déductions dans ce [20] domaine, qu'il en est arrivé à affirmer que la rotation même de la Terre autour du Soleil n'est qu'une hypothèse plus commode que l'hypothèse inverse, mais non point plus vraie, car elle impliquerait sans cela l'existence d'un espace absolu.

Certains polémistes peu avertis ont même,—on s'en souvient,—voulu tirer argument de cette démonstration poincariste pour justifier la condamnation de Galilée. Rien de plus amusant que les efforts faits alors par l'illustre mathématicien-philosophe pour se défendre de ce grief, et, ma foi, il faut bien reconnaître que la défense ne fut pas parfaitement convaincante. C'est qu'on ne fait pas à l'agnosticisme sa part.

Poincaré est donc à la tête de ceux pour qui l'espace n'est rien qu'une propriété que nous donnons aux objets. Pour lui, la notion que nous en avons n'est, si j'ose dire, que la résultante héréditaire des tâtonnements sensuels par quoi nous essayons péniblement d'embrasser le monde extérieur à un moment donné.

Après l'Espace, le Temps. A cet égard aussi les objections du relativisme philosophique étaient depuis longtemps dans l'air. Mais c'est Poincaré qui leur a donné leur forme définitive. Nous ne le suivrons pas dans ses lumineuses démonstrations qui sont bien connues.

Retenons-en seulement que, pour le temps comme pour l'espace, on peut supposer un rétrécissement ou un allongement de l'échelle, auquel nous serions tout à fait insensibles et qui semble montrer l'impossibilité, pour les hommes, de concevoir un temps absolu.

[21] Si quelque génie malicieux s'amusait une nuit à rendre mille fois plus lents tous les phénomènes de l'Univers, nous n'aurions aucun moyen de nous en apercevoir à notre réveil et le monde ne nous paraîtrait pas changé. Et pourtant chacune des heures marquées par nos horloges durerait mille fois plus qu'une des heures anciennes. Les hommes vivraient mille fois plus longtemps, et n'en sauraient rien, car leurs sensations seraient ralenties d'autant.

Lorsque Lamartine s'écriait: «O temps, suspends ton vol!» il proférait une chose charmante, mais qui n'était peut-être qu'une niaiserie. Si le temps avait obéi à cette objurgation passionnée, à cet ordre,—les poètes ne doutent de rien!—Lamartine et Elvire n'eussent pu le savoir ni en jouir. Le batelier du lac du Bourget qui promenait les deux amoureux, n'eût réclamé le paiement d'aucune heure supplémentaire; et pourtant il aurait, de ses rames, frappé bien plus longtemps les flots harmonieux.

Si j'ose résumer tout cela d'un mot moins paradoxal qu'il ne semblera à première vue: aux yeux des relativistes ce sont les mètres qui créent l'espace, les horloges qui créent le temps.

Tout cela, Poincaré et d'autres l'ont soutenu bien longtemps avant Einstein, et c'est faire tort à la vérité que de le lui attribuer. Je sais bien qu'on ne prête qu'aux riches, mais c'est aussi faire injure aux riches que de leur prêter ce dont ils n'ont que faire, ce dont ils n'ont pas besoin pour être riches.

[22] Il est d'ailleurs un point où Galilée et Newton, tout en croyant à l'existence de l'espace et du temps absolus, admettaient déjà une certaine relativité. C'est l'impossibilité, reconnue par eux, de distinguer les uns des autres, les mouvements de translation uniformes; c'est l'équivalence de toutes ces translations; c'est par conséquent l'impossibilité de mettre en évidence une translation absolue.

C'est cela qu'on appelle le principe de relativité classique.

Un fait imprévu a contribué à porter ces questions sur un plan nouveau, et amené Einstein à donner une extension inattendue au principe de relativité de la mécanique classique: c'est le résultat d'une expérience célèbre de Michelson, qu'il importe de décrire brièvement.

On sait que les rayons lumineux se propagent dans le vide interastral; c'est ce qui nous permet d'apercevoir les étoiles. Cela a conduit depuis longtemps les physiciens à admettre que ces rayons se propagent dans un milieu dénué de masse et d'inertie, infiniment élastique, n'opposant aucune résistance au déplacement des corps matériels qu'il pénètre de toute part. Ce milieu les savants l'appellent l'éther. La lumière s'y propage à la manière des ondes dans l'eau, avec une vitesse voisine de 300 000 kilomètres par seconde et que je désignerai abréviativement par la lettre V.

[23] La Terre circule autour du Soleil dans un véritable océan d'éther et avec une vitesse de translation d'environ 30 kilomètres par seconde. A cet égard la rotation de la Terre peut être négligée car elle imprime à la surface terrestre dans l'éther une vitesse inférieure à 2 kilomètres par seconde.

Depuis longtemps la question suivante s'est posée: la Terre entraîne-t-elle, dans son mouvement orbital autour du Soleil, l'éther qui est à son contact, de même qu'une éponge lancée d'une fenêtre emporte avec elle l'eau dont elle est imbibée? L'expérience a montré, ou plutôt les expériences ont montré (elles sont variées et concordantes) que la question doit être résolue par la négative.

Cela a été établi d'abord par les observations astronomiques. Il existe en astronomie un phénomène bien connu, découvert par Bradley, et qu'on appelle l'aberration. Il consiste en ceci: lorsqu'on observe une étoile avec une lunette, l'image de l'étoile ne se forme pas exactement dans la direction de la visée. En voici la raison: pendant que les rayons lumineux de l'étoile, qui ont pénétré dans la lunette, parcourent celle-ci dans sa longueur, la lunette s'est légèrement déplacée, entraînée qu'elle est par le mouvement de la Terre. Au contraire, le rayon lumineux dans la lunette n'a pas participé à ce mouvement, ce qui cause précisément la petite déviation appelée aberration. Preuve que le milieu dans lequel se propage la lumière, l'éther qui remplit la lunette et entoure la Terre, ne participe pas au mouvement de celle-ci.

[24] Beaucoup d'autres expériences ont établi d'une manière aussi nette que l'éther, qui sert de véhicule aux ondes lumineuses n'est pas entraîné par la Terre dans son mouvement. Mais alors, puisque la Terre est mouvante dans l'éther, puisqu'elle y avance comme un navire dans un lac immobile (et non pas comme un flotteur porté par le courant d'un fleuve), il doit être possible de mettre en évidence cette vitesse de la Terre par rapport à l'éther.

Un des moyens qu'on peut imaginer dans ce dessein est le suivant. On sait que la Terre tourne de l'Ouest à l'Est sur elle-même et dans le même sens autour du Soleil. Par conséquent, au milieu de la nuit, la révolution de la Terre autour du Soleil l'entraîne dans un sens tel que Paris se déplace, d'Auteuil vers Charenton, avec une vitesse d'environ 30 kilomètres par seconde (le jour, c'est le contraire, Paris se déplace autour du Soleil, de Charenton vers Auteuil). Supposons donc qu'au milieu de la nuit un physicien placé à Auteuil envoie un signal lumineux; le physicien de Charenton (ceci, encore un coup, est une hypothèse), qui mesure la vitesse de ce rayon lumineux, devra trouver qu'elle est égale à V − 30 kilomètres.

En effet, par suite du mouvement de la Terre, Charenton fuit devant le rayon lumineux. Par conséquent, puisque celui-ci se propage dans un milieu, dans un éther qui ne participe pas au mouvement de la Terre, l'observateur de Charenton devra trouver que ce rayon lui arrive avec une vitesse plus faible que si la Terre [25] était immobile. C'est un peu comme un train rapide devant lequel fuirait un observateur à bicyclette; si le train rapide fait 30 mètres à la seconde, si le cycliste fait 3 mètres à la seconde, la vitesse du train par rapport au cycliste sera 30 − 3 = 27 mètres à la seconde; elle serait nulle si train et cycliste avaient même vitesse.

Au contraire, si le cycliste va à la rencontre du train, la vitesse du train par rapport à lui sera 30 + 3 = 33 mètres par seconde. Pareillement, si c'est le physicien de Charenton, qui au milieu de la nuit, envoie un signal lumineux, et le physicien d'Auteuil qui le reçoive, celui-ci devra trouver que ce rayon lumineux possède une vitesse égale à V + 30 kilomètres.

On peut encore exprimer autrement tout cela. Supposons qu'il y ait exactement 12 kilomètres entre l'observateur d'Auteuil et celui de Charenton. Pendant que le rayon lumineux venu d'Auteuil se propage vers Charenton, Charenton fuit devant lui d'une petite quantité. Par conséquent ce rayon aura parcouru un peu plus de 12 kilomètres avant d'arriver au physicien de Charenton. Il aura au contraire parcouru un peu moins dans le cas contraire.

Or, appliquant une belle idée française de Fizeau, le physicien américain Michelson a réussi à mesurer avec une grande précision les longueurs, au moyen des franges d'interférence de la lumière. Toute variation de la longueur mesurée se traduit par un déplacement d'un certain nombre de ces franges que l'on peut observer facilement avec un microscope.

[26] Imaginons maintenant qu'au lieu d'expérimenter entre Charenton et Auteuil, nos deux physiciens opèrent dans les limites d'un laboratoire. Imaginons qu'ils mesurent, au moyen des franges d'interférence, l'espace parcouru par un rayon lumineux produit dans ce laboratoire, et selon qu'il s'y propage dans le sens du mouvement de la Terre ou dans le sens contraire. Nous aurons ainsi, réduite à ses éléments essentiels, et simplifiée pour la clarté de cet exposé, la célèbre expérience de Michelson. On devrait trouver de la sorte une différence facilement mesurable avec l'appareil précis utilisé.

Eh bien! pas du tout. Contrairement à toute attente, et à la profonde stupéfaction des physiciens, on a trouvé que la lumière se propage rigoureusement avec la même vitesse lorsque celui qui la reçoit s'éloigne d'elle avec la vitesse de la Terre, ou au contraire lorsqu'il s'en rapproche avec cette vitesse. Conséquence inéluctable: l'éther participe au mouvement de la Terre. Mais nous venons de voir que d'autres expériences, non moins précises, avaient établi que l'éther ne participe pas au mouvement de la Terre.

C'est de cette contradiction, du choc de ces deux faits inconciliables et pourtant réels, qu'est sortie la splendide synthèse d'Einstein, de même que, fulgurante, l'étincelle jaillit du choc de deux silex heurtés.

Après tout, la mathématique n'est pas, n'a jamais été et ne sera jamais autre chose qu'un langage particulier, une sorte de sténographie de la pensée et du raisonnement. Son objet est de franchir les méandres [28] compliqués des raisonnements superposés, avec une rapide hardiesse que ne connaissent pas la lourdeur et la lenteur mérovingiennes des syllogismes exprimés par des mots.

Si paradoxal que cela puisse paraître à ceux qui considèrent les mathématiques comme étant par elles-mêmes une source de découverte, on n'en sortira jamais autre chose que ce qui était implicitement inhérent aux données jetées dans la double mâchoire des équations. Pour employer une image triviale qu'on me pardonnera, j'espère, les raisonnements mathématiques sont tout à fait analogues à ces machines qu'on voit à Chicago—à ce que disent les hardis explorateurs de l'Amérique,—à l'entrée desquelles on met des bestiaux vivants et qui restituent à la sortie d'odorantes charcuteries. Nul parmi les spectateurs n'eût pu ou du moins n'eût voulu tenter d'absorber l'animal vivant, tandis que, sous la forme où il se présente à la sortie, il est immédiatement assimilable et digéré. Pourtant ceci n'est que cela convenablement trituré. Ce n'est pas autre chose que font les mathématiques. Elles extraient des données toute leur substantifique moelle, par le moyen d'une machinerie merveilleuse. Celle-ci est efficace là où les rouages du raisonnement verbal, là où l'imbrication des syllogismes seraient bientôt arrêtés et coincés.

Faut-il en conclure que les mathématiques ne sont pas, à proprement parler, des sciences? Faut-il du moins en conclure qu'elles ne sont sciences qu'autant [29] qu'elles se modèlent sur la réalité et se nourrissent de données expérimentales, puisque «l'expérience est la source unique de la vérité», et puisque la science est la recherche de la vérité? Je me garderai bien de répondre à cela, étant de ceux qui pensent que tout est matière de science. Cette question n'en méritait pas moins d'être posée, car on a peut-être un peu trop tendance chez nous à considérer une éducation purement mathématique comme constituant une éducation scientifique. Rien n'est plus faux. La mise en équations n'est par elle-même qu'une forme abréviative donnée au langage et à la pensée logique. Elle ne peut rien nous apprendre intrinsèquement sur le monde extérieur; elle ne peut nous renseigner sur lui qu'autant qu'elle s'y lie docilement. C'est de la mathématique surtout qu'on pourrait dire: naturæ non imperatur nisi parendo.

Les théories d'Einstein ne sont-elles, comme certaines personnes mal informées l'ont prétendu, qu'un jeu de formules transcendantes (et j'entends ce mot à la fois dans le sens des mathématiciens et dans celui des philosophes)? Si elles n'étaient qu'un vertigineux édifice mathématique où les x enroulent leurs volutes en arabesques étourdissantes, où les intégrales au col de cygne dessinent des motifs Louis XV, elles ne seraient pas, elles ne seraient guère intéressantes pour le physicien, pour celui qui regarde et examine la nature des choses avant d'en disserter. Elles ne seraient, comme toutes les métaphysiques cohérentes, qu'un [30] système plus ou moins plaisant, mais dont on ne peut démontrer l'exactitude ou la fausseté.

La théorie d'Einstein est bien autre chose, bien plus que cela. C'est sur les faits qu'elle se fonde. C'est aussi à des faits, à des faits nouveaux qu'elle aboutit. Jamais une doctrine philosophique, jamais non plus une construction mathématique purement formelle n'ont fait découvrir des phénomènes nouveaux. Parce qu'elle en a fait découvrir la théorie d'Einstein n'est ni l'une ni l'autre. Là est ce qui différencie la théorie scientifique de la spéculation pure et qui fait, j'ose le dire, la supériorité de celle-là.

Ainsi qu'un audacieux pont suspendu jeté à travers l'abîme, la synthèse d'Einstein s'appuie d'un côté sur des phénomènes expérimentaux, pour aboutir, par son côté opposé, à d'autres phénomènes jusque-là insoupçonnés, et que grâce à elle on découvre. Entre ces deux solides piliers phénoménaux, le raisonnement mathématique est l'enchevêtrement merveilleux des milliers de croisillons d'acier qui dessinent l'architecture élégante et translucide du pont. Il est cela, il n'est que cela. Mais l'agencement des poutrelles et des croisillons pourrait être différent et le pont réunir quand même,—avec moins de gracieuse légèreté peut-être,—les faits où il s'arc-boute des deux parts.

Bref le raisonnement mathématique n'est en physique qu'une induction, dans un langage particulier, entre des prémisses expérimentales et des conclusions justiciables de l'expérience et vérifiables par elle. Or il [31] n'est point de langage qui,—tant bien que mal,—ne puisse être traduit dans un autre langage. Les hiéroglyphes eux-mêmes ont dû céder devant Champollion. C'est pourquoi, finalement, je suis persuadé que les difficultés mathématiques des théories d'Einstein seront un jour remplacées par un jeu de formules plus simples et plus accessibles. C'est pourquoi je crois aussi qu'il est dès maintenant possible de donner, au moyen du langage ordinaire, une idée peut-être un peu superficielle mais pourtant exacte dans les grandes lignes, de ce merveilleux monument einsteinien où toutes les conquêtes de la science viennent se classer, ainsi qu'en un admirable musée, selon un ordre nouveau et d'une splendide unité. Essayons.

On peut récapituler très brièvement de la manière suivante ce qui a été l'origine, la tranchée de départ du système d'Einstein: 1^o l'observation des astres prouve que l'espace interplanétaire n'est pas vide, mais est occupé par un milieu particulier, l'éther, dans lequel se propagent les ondes lumineuses; 2^o l'existence de l'aberration et d'autres phénomènes semble prouver que l'éther n'est pas entraîné par la Terre dans son mouvement circumsolaire; 3^o l'expérience de Michelson semble prouver au contraire que l'éther est entraîné par la Terre dans ce mouvement.

[32] Cette contradiction entre des faits également bien établis a fait pendant des années le désespoir et l'étonnement des physiciens. Elle fut le nœud gordien de la science. On chercha longtemps et en vain à le dénouer, jusqu'à ce qu'Einstein, d'un seul coup de son esprit merveilleusement aiguisé, le tranche net.

Pour comprendre comment cela se fit,—et là est le point vital de tout le système,—il nous faut revenir un peu sur les conditions exactes de la fameuse expérience de Michelson.

J'ai indiqué dans le chapitre précédent que Michelson s'est proposé d'étudier la vitesse de propagation d'un rayon lumineux que l'on produit au laboratoire et qui est dirigé de l'Est à l'Ouest ou de l'Ouest à l'Est, c'est-à-dire suivant la direction même où la Terre se meut à la vitesse de 30 kilomètres environ par seconde, dans son mouvement autour du Soleil.

Mais en réalité l'expérience de Michelson est un peu plus compliquée que cela et il importe d'y revenir.

En fait, elle revient à disposer dans le laboratoire quatre miroirs équidistants et se faisant face deux à deux. Deux des miroirs opposés sont placés suivant la direction Est-Ouest, direction du mouvement de translation de la Terre autour du Soleil; les deux autres sont placés suivant la direction perpendiculaire à la précédente, la direction Nord-Sud. On produit deux rayons lumineux se propageant respectivement suivant les directions des deux couples de miroirs. Le rayon provenant du miroir Est va au miroir Ouest, est [33] réfléchi par lui et revient au miroir Est. Ce rayon est amené à coïncider avec celui qui a fait le trajet aller et retour entre les miroirs Nord-Sud; il interfère avec lui en produisant des franges d'interférences, qui, ainsi que je l'ai expliqué, permettent de connaître exactement la différence des trajets parcourus par les deux rayons entre les miroirs. S'il se produisait une variation de la différence entre ces deux distances, on verrait immédiatement se déplacer un certain nombre des franges d'interférences, ce qui fournirait la grandeur de cette variation.

Et maintenant une analogie va nous faire comprendre ce qui se passe. Supposons qu'un vent violent et régulier Est-Ouest souffle au-dessus de Paris et qu'un avion se propose de faire le trajet d'Auteuil à Charenton et retour sans escale, c'est-à-dire contre le vent à l'aller et avec le vent en poupe au retour. 12 kilomètres séparent Auteuil de Charenton. Supposons qu'en même temps un autre avion identique au premier se propose de franchir, en partant également d'Auteuil, un trajet aller et retour entre Auteuil et un point situé à 12 kilomètres au Nord. De la sorte ce deuxième avion aura, à l'aller comme au retour, un trajet perpendiculaire à la direction du vent. Ces deux avions étant supposés partir en même temps et faire demi-tour instantanément, seront-ils de retour en même temps à Auteuil, et sinon, quel est celui qui aura fini son double parcours le premier?

S'il n'y avait pas de vent, il est clair que les deux [34] avions seraient de retour en même temps, puisqu'ils parcourent tous deux 24 kilomètres à la même vitesse, que je suppose, pour fixer les idées, de 200 mètres à la seconde.

Mais il n'en sera plus de même s'il y a du vent soufflant dans la direction Est-Ouest, ainsi que je l'ai admis. Il est facile de voir, dans ces conditions, que l'avion qui va d'Auteuil à Charenton et retour aura fini son parcours plus tard que l'autre avion. En effet, imaginons, pour fixer les idées, que le vent ait la même vitesse que l'avion (200 mètres par seconde). L'avion, qui va perpendiculairement au vent, sera déporté vers l'Ouest de 12 kilomètres, pendant qu'il franchit lui-même 12 kilomètres du Sud au Nord. Il aura donc franchi dans le vent une distance réelle égale à la diagonale d'un carré de 12 kilomètres de côté. Au lieu de franchir 24 kilomètres, il en aura franchi réellement 34 dans le vent, qui est le milieu par rapport auquel il possède sa vitesse.

En revanche, l'avion qui part d'Auteuil vers l'Est n'arrivera jamais à Charenton, puisqu'il est déporté vers l'Ouest, chaque seconde, d'une quantité égale à celle dont il progresse vers l'Est; il restera sur place; il lui faudrait donc franchir dans le vent une distance infinie pour effectuer son voyage.

Si, au lieu de supposer au vent une vitesse égale à celle de l'avion (ce qui est un cas limite choisi pour la clarté de ma démonstration), je lui avais attribué une vitesse plus faible, on trouverait pareillement, et [35] par un calcul très simple, que, pour effectuer son trajet aller et retour, l'avion Nord-Sud parcourt dans le vent un espace moins grand que l'avion Est-Ouest.

Remplaçons nos avions par des rayons lumineux, le vent par l'éther, et nous aurons presque exactement les conditions de l'expérience de Michelson. Un courant d'éther, un vent d'éther (puisque celui-ci a été antérieurement reconnu immobile par rapport à la translation terrestre), va de l'un à l'autre de nos deux miroirs Est-Ouest. Donc le rayon lumineux qui fait le trajet aller et retour entre ces deux miroirs doit parcourir dans l'éther un trajet plus long que le rayon qui fait le trajet aller et retour entre les miroirs Nord-Sud. Comment mettre en évidence cette différence, assurément très faible, puisque la Terre a une vitesse infime par rapport à celle de la lumière, 10 000 fois plus petite?

Il y a pour cela un moyen très simple, un de ces artifices ingénieux chers à la malice des physiciens, un de ces procédés différentiels dont l'élégance et la netteté donnent toute sécurité.

Supposons que mes quatre miroirs soient collés, placés rigidement sur un plateau un peu semblable aux tourniquets numérotés des loteries foraines. Supposons qu'on puisse faire tourner ce plateau à volonté, sans choc et sans le déformer, ce qui est aisé si on le fait flotter sur un bain de mercure. J'observe à la loupe les franges d'interférences immobiles qui définissent la différence des trajets parcourus par mes [36] rayons lumineux Nord-Sud et Est-Ouest. Puis, sans perdre de l'œil ces franges, je fais tourner mon plateau d'un quart de cercle. Cette rotation fait que les miroirs qui étaient Est-Ouest deviennent Nord-Sud et réciproquement. Le double trajet parcouru par le rayon lumineux Nord-Sud est devenu Est-Ouest, s'est donc soudain allongé; au contraire, le double trajet du rayon Est-Ouest est devenu Nord-Sud, s'est donc soudain raccourci. Les franges d'interférences, qui indiquent la différence de longueur de ces deux trajets, laquelle a soudain beaucoup varié, doivent nécessairement s'être déplacées, et d'une grande quantité, ainsi que le montre le calcul.

Eh bien! pas du tout. On constate une immobilité complète des franges. Elles n'ont pas plus bougé que souches. C'est renversant, révoltant même, car enfin la précision de l'appareil est telle que, si la Terre n'avançait dans l'éther qu'à la vitesse de 3 kilomètres par seconde (dix fois moins que sa vitesse réelle!), le déplacement des franges serait suffisant pour manifester cette vitesse.

Lorsque fut connu le résultat négatif de cette expérience, ce fut presque de la consternation parmi les physiciens. Puisque l'éther,—cela avait été prouvé par l'observation,—n'était pas entraîné par la Terre, comment était-il possible qu'il se comportât comme [37] s'il avait participé à son mouvement? Casse-tête chinois, qui ébranla mainte tête chenue et vénérable.

Il fallait à toute force sortir de cette inexplicable contradiction, venger ce paradoxal pied de nez que les faits décochaient aux prévisions les plus sûres du calcul. C'est ce qu'on fit. Comment? Mais par la méthode habituelle en pareil cas, par des hypothèses supplémentaires. Les hypothèses sont dans la science une sorte de mortier souple et rapidement durci à l'air libre, qui permet d'une part de joindre les blocs disparates d'un édifice, d'autre part de remplir par du faux, que le passant superficiel prendra demain pour de la pierre de taille, les brèches creusées dans la muraille par les projectiles adventices. Et c'est parce que les hypothèses sont dans la science quelque chose qui ressemble à cela, que les meilleures théories scientifiques sont celles dont l'assemblage comporte le moins d'hypothèses.

Mais j'ai tort d'écrire, à propos de tout ceci, ce mot au pluriel, car il se trouva finalement qu'une seule et unique hypothèse permettait, à l'exclusion de toute autre, d'expliquer convenablement le résultat négatif de l'expérience de Michelson. Ceci d'ailleurs est rare et remarquable, car en général les hypothèses poussent comme des champignons dans chaque coin un peu sombre de la science, et on en trouve tout de suite vingt différentes pour expliquer la moindre incertitude.

Cette hypothèse unique, qui semblait pouvoir tirer les physiciens de l'embarras où les avait plongés Michelson, fut imaginée d'abord par le savant irlandais Fitzgerald, [38] puis reprise et fécondée par l'illustre Hollandais Lorentz, le Poincaré néerlandais, qui est un des plus merveilleux cerveaux de ce temps, et sans qui Einstein n'aurait pas plus existé que Képler sans Copernic et Tycho-Brahé.

Voici maintenant en quoi consiste l'hypothèse aussi simple qu'étrange de Fitzgerald-Lorentz....

Mais auparavant, une remarque importante s'impose. Beaucoup de bons esprits ont,—d'ailleurs après coup,—prétendu que le résultat de l'expérience de Michelson ne pouvait être que négatif a priori. En effet,—ont-ils raisonné, ou à peu près,—le principe de relativité classique, celui que Galilée et Newton connaissaient déjà, veut qu'il soit impossible à un observateur participant à la translation uniforme d'un véhicule, de mettre en évidence, par des faits observés sur le véhicule, les mouvements de celui-ci. Cela fait que quand deux navires ou deux trains se croisent[3], il est impossible aux passagers de connaître lequel est en mouvement, lequel va plus vite: tout ce qu'ils peuvent connaître, c'est la vitesse de l'un des trains ou des navires par rapport à l'autre. On ne peut connaître que des vitesses relatives.

Or, ont dit les bons esprits auxquels je fais allusion, si l'expérience de Michelson avait donné un résultat positif, elle nous aurait fait connaître la vitesse absolue de la [39] Terre dans l'espace. Ce résultat aurait été contraire au principe de relativité de la philosophie et de la mécanique classiques qui est une vérité d'évidence. Donc, il ne pouvait être que négatif.

Il y a là, ainsi qu'on va voir, une ambiguïté et,—si j'ose ainsi m'exprimer,—une erreur de raisonnement à laquelle il semble que n'aient pas échappé certains physiciens remarquables et notamment le professeur Eddington, qui est pourtant le plus averti des einsteiniens anglais. Par lui furent organisées les observations de l'éclipse du 29 mai 1919 qui ont fourni, comme nous verrons, la vérification la plus frappante des inductions d'Einstein.

Tout d'abord, si l'expérience de Michelson avait donné un résultat positif, ce qu'elle aurait mis en évidence, c'est la vitesse de la Terre par rapport à l'éther. Mais, pour que cette vitesse fût une vitesse absolue, il faudrait que l'éther fût identique à l'espace. Rien n'est moins certain que cette identité, et la preuve, c'est que nous pouvons très bien concevoir entre deux astres un espace, ou, pour mieux dire, une discontinuité, vide d'éther même, et à travers laquelle ne se propagerait ni la lumière, ni aucune des formes d'énergie connues.

Lorsque Eddington dit qu'«il est légitime et rationnel», qu'il est «inhérent aux lois fondamentales de la nature», qu'on ne puisse déceler un mouvement des objets par rapport à l'éther, que cela est certain, «même si les preuves expérimentales sont insuffisantes», il affirme une chose qui ne serait évidente que si l'identité [40] de l'espace et de l'éther était elle-même évidente. Or, il n'en est rien. Si l'expérience de Michelson avait donné un résultat positif, si on avait décelé une vitesse de la Terre, aurait-on décelé une vitesse par rapport à un point de repère absolu? Nullement. Il se peut, il se pourrait très bien que l'Univers stellaire que nous connaissons, avec ses centaines de milliers de Voies lactées que la lumière ne franchit qu'en des millions d'années, il se peut que tout cela soit le contenu d'une bulle d'éther qui roule dans un abîme vide d'éther et semé çà et là d'autres univers, d'autres gouttes d'éther gigantesques dont rien, dont aucun rayon lumineux ne nous viendra jamais. Ceci n'est en tout cas pas inconcevable. Mais alors, l'éther ayant les propriétés que lui attribue la physique classique, si le mouvement de la Terre par rapport à lui avait pu être décelé, ce n'est pas un mouvement absolu qu'on aurait connu, c'est tout au plus un mouvement par rapport au centre de gravité de notre Univers à nous, point de repère lui-même irréductible à un autre absolument immobile. Le principe de relativité classique n'aurait été en rien choqué.

Le résultat de l'expérience de Michelson pouvait donc, dans ces hypothèses, être aussi bien positif que négatif sans heurter,—quoi qu'on en ait dit,—le relativisme classique. En fait, il s'est trouvé négatif, et voilà tout: l'expérience a prononcé, mais elle seule pouvait prononcer.

Ces nuances n'ont pas échappé à Poincaré, qui disait [41] notamment: «Par véritable vitesse de la Terre, j'entends, non sa vitesse absolue, ce qui n'a aucun sens, mais sa vitesse par rapport à l'éther....» L'existence possible d'une vitesse décelable par rapport à l'éther n'apparaissait donc nullement comme une absurdité à celui qui a écrit: «Quiconque parle de l'espace absolu emploie un mot vide de sens.»

Il est assez digne de remarque que, dans tout ceci, la démarche de la pensée de Poincaré a marqué quelque hésitation. A propos d'expériences analogues à celles de Michelson, il s'écriait: «Je sais ce qu'on va dire, ce n'est pas la vitesse absolue qu'on mesure, c'est la vitesse par rapport à l'éther. Que cela est peu satisfaisant! Ne voit-on pas que du principe ainsi compris on ne pourra plus rien tirer?» D'où il ressort que Poincaré en dépit de lui-même, et tout en s'en défendant, avait une tendance à trouver «peu satisfaisante» la discrimination de l'espace et de l'éther.

J'avoue que l'argument de Poincaré ne me paraît pas, lui non plus, tout à fait satisfaisant, ou du moins convaincant. «La nature, a dit Fresnel, ne se soucie pas des difficultés analytiques.» Je pense qu'elle ne se soucie pas non plus des difficultés philosophiques ou purement physiques. Penser qu'une conception des phénomènes est d'autant plus adéquate au réel qu'elle est plus «satisfaisante», qu'elle s'adapte mieux aux infirmités de notre esprit, n'est peut-être pas un criterium inattaquable. Sinon il faudrait bon gré mal gré en arriver à penser que l'Univers est nécessairement [42] adapté aux catégories de notre esprit, qu'il est constitué de manière à nous causer le moins de perplexités possibles. Ce serait, par un chemin détourné, un étrange retour au finalisme et à l'orgueil anthropocentriques. Le fait que les voitures n'y passent pas, et que les passants y doivent rebrousser chemin, ne prouve pas qu'il n'y ait pas des impasses dans nos villes. Il y a peut-être et même probablement aussi des impasses dans l'Univers considéré comme objet de science.

Assurément on peut me répondre: ce n'est pas l'Univers qui est adapté à notre esprit, mais au contraire celui-ci à celui-là par l'évolution nécessaire due au frottement réciproque de l'un sur l'autre. Notre esprit doit évoluer en s'adaptant au mieux à l'Univers, c'est-à-dire de sorte que le principe de moindre action de Fermat,—qui est peut-être le plus profond principe du monde physique, biologique et moral,—soit réalisé. Et alors les conceptions les plus économiques, les plus simples sont bien les plus adéquates à la réalité.

Oui, mais qu'est-ce qui prouve que notre évolution conceptuelle est achevée et parfaite, surtout quand il s'agit de phénomènes auxquels notre organisme est insensible?

L'expérience, seule, a prouvé et était capable de prouver qu'on ne peut mesurer la vitesse d'un objet par rapport à l'éther. Mais enfin, elle l'a bien prouvé.

[43] Après tout, puisqu'il est évidemment dans la nature des choses que nous ne puissions déceler de mouvement absolu, n'est-ce pas parce que la vitesse de la Terre par rapport à l'éther constitue une vitesse absolue, que nous n'avons pu la déceler? Peut-être, mais c'est indémontrable. Si oui,—mais il n'est pas sûr que ce soit oui,—c'est finalement l'expérience, seule source de la vérité, qui tend à nous montrer ainsi, indirectement, que l'éther est réellement identique à l'espace. En ce cas un espace vide d'éther, ou dans lequel rouleraient des bulles d'éther, cesse d'être concevable, et il n'existe rien qu'une masse unique d'éther où baignent les astres. En un mot, le résultat négatif de l'expérience de Michelson ne pouvait être déduit a priori de l'identité problématique de l'espace absolu et de l'éther. Mais ce résultat négatif ne permet pas d'exclure a posteriori cette identité.

Il importe que nous revenions maintenant à nos moutons, je veux dire à l'hypothèse de Fitzgerald-Lorentz qui explique le résultat de l'expérience de Michelson, et qui fut en quelque sorte le tremplin d'où Einstein prit son essor. Voici cette hypothèse.

Le résultat de l'expérience est celui-ci: quand le parcours aller et retour d'un rayon lumineux entre deux miroirs est transversal au mouvement de la Terre à travers l'éther, et qu'on le rend parallèle à ce mouvement, on devrait constater que ce parcours a été allongé. Or, on constate qu'il n'en est rien. Cela provient, d'après Fitzgerald et Lorentz, de ce que les deux miroirs se sont [44] rapprochés dans le second cas, autrement dit de ce que le support sur lequel ils sont fixés s'est contracté dans le sens du mouvement de la Terre, et s'est contracté d'une quantité qui compense exactement l'allongement, qu'on aurait dû observer, du parcours des rayons lumineux.

Or, en refaisant l'expérience avec les appareils les plus variés, on constate que le résultat est toujours le même (aucun déplacement des franges). Donc, la nature de la matière formant l'instrument (métal, verre, pierre, bois, etc.) n'a aucune influence. Donc, tous les corps subissent, dans le sens de leur vitesse par rapport à l'éther, un raccourcissement égal, une contraction pareille. Cette contraction est telle qu'elle compense précisément l'allongement du trajet des rayons lumineux entre deux points de la matière. Cette contraction est donc d'autant plus grande que la vitesse des corps par rapport à l'éther est plus grande.

Telle est l'explication proposée par Fitzgerald. Elle sembla au premier abord tout à fait étrange et arbitraire, et pourtant il n'apparaissait pas d'autre moyen d'expliquer le résultat de l'expérience de Michelson.

D'ailleurs, si on y réfléchit, cette contraction devient bientôt une chose moins extraordinaire, moins choquante pour le sens commun qu'il ne semblait d'abord. Si on jette très vite, contre un obstacle, un objet déformable, tel qu'un de ces petits ballons de baudruche que les enfants tiennent en laisse, on constate qu'il est légèrement déformé par l'obstacle, et précisément dans le sens de la contraction Fitzgerald-Lorentz. Le ballon [45] cesse d'être sphérique, il s'aplatit un peu et de telle sorte que son diamètre dans la direction de l'obstacle devient plus petit. C'est à peu près, avec plus de violence, le même phénomène qui se produit lorsqu'un grain de plomb ou une balle vient s'aplatir sur un blindage. Si donc les corps solides sont déformables,—et ils le sont, puisque le froid suffit à resserrer leurs molécules,—il n'est, après tout, pas absurde, pas impossible d'imaginer qu'un violent vent d'éther les déforme.

Mais il est beaucoup moins admissible que cette déformation soit identique, soit égale, dans des conditions données, pour tous les corps quelle que soit la matière dont ils sont formés. Notre petit ballon de tout à l'heure ne serait pas du tout aplati autant, s'il était en acier au lieu d'être en baudruche.

Enfin, il y a dans cette explication quelque chose de tout à fait invraisemblable, quelque chose qui choque à la fois le bon sens et sa caricature, le sens commun. Est-il admissible que la contraction des objets, quelles que soient les circonstances des expériences (et on les a beaucoup variées), compense toujours exactement l'effet optique qu'on cherche à déceler? Est-il admissible que la nature agisse comme si elle jouait à cache-cache avec nous? Par quel mystérieux hasard se trouverait-il pour chaque phénomène une circonstance spéciale, providentiellement et exactement compensatrice?

Évidemment, il doit y avoir quelque affinité, quelque [46] liaison d'abord inaperçue, qui lie étroitement la mystérieuse contraction matérielle de Fitzgerald et l'allongement, compensé par elle, des trajets lumineux. Nous verrons tout à l'heure comment Einstein a élucidé le mystère, démonté le mécanisme jumelé qui lie les deux phénomènes, et projeté sur tout cela un faisceau de brillante lumière. Mais n'anticipons pas....

Elle est d'ailleurs extrêmement faible, la contraction de l'appareil dans l'expérience de Michelson. Elle l'est tellement que si l'instrument avait une longueur égale au diamètre de la Terre, c'est-à-dire 12 000 kilomètres, il ne serait raccourci dans le sens de la translation terrestre que de 6 centimètres et demi! C'est dire que ce raccourcissement ne pourrait en aucun cas, étant donnée son extrême petitesse, être mesurable au laboratoire.

Il y a une autre raison à cela: même si l'appareil de Michelson était raccourci de plusieurs centimètres (c'est-à-dire même si la Terre avait une translation des milliers de fois plus rapide), cela ne pourrait être ni mesuré ni constaté. En effet, les mètres dont nous nous servirions pour faire cette mesure seraient raccourcis proportionnellement d'autant. La déformation d'un objet terrestre par la contraction de Fitzgerald-Lorentz ne peut être en aucun cas mise en évidence par un observateur d'ici-bas. Seul pourrait la constater un observateur ne participant pas à la translation de la Terre et placé par exemple sur le Soleil, ou sur une planète lente, comme Jupiter ou Saturne.

[47] Micromégas, avant que de quitter, pour nous faire visite, sa planète d'origine, aurait donc pu, par des moyens optiques, constater que notre globe est raccourci de quelques centimètres dans la direction de son orbite, supposé que l'aimable héros voltairien fût muni d'appareils de triangulation infiniment plus précis que ceux de nos géodésiens et de nos astronomes. Arrivé sur la Terre, Micromégas, muni des mêmes appareils précis, eût été dans l'impossibilité de constater à nouveau ce raccourcissement. Il en eût éprouvé assurément une grande surprise jusqu'à ce que, rencontrant Einstein, celui-ci lui eût expliqué,—comme il fera pour nous,—et élucidé le mystère.

Mais je n'ai hélas! pas le loisir ni l'espace,—car c'est ici surtout que l'espace est relatif et sans cesse raccourci par le mouvement même de la plume,—pour décrire ce qu'aurait pu être le dialogue de Micromégas et d'Einstein. Peut-être d'ailleurs, pour rester dans la vraisemblance du pastiche, ce dialogue eût-il été fort superficiel, car—ceci dit confidentiellement,—je crois bien que Voltaire, encore qu'il en ait fort discuté, n'a jamais trop bien compris Newton, lequel était moins difficile qu'Einstein. Mme du Chatelet non plus, dont on a vanté à tort la traduction des Principes... des immortels Principes.... Cette traduction fourmille de non-sens prouvant que, si elle savait bien le latin, l'Egérie du philosophe n'entendait guère le Newton. Mais tout ceci est une autre affaire, comme dit Kipling.

[48]

Selon l'heure et la saison où l'on fait l'expérience de Michelson et les expériences analogues, la translation de l'appareil dans l'éther est plus ou moins rapide. Comme la compensation se produit toujours exactement, on peut se proposer de calculer la loi exacte qui règle la contraction en fonction des vitesses, et rend celle-là, ainsi qu'on le constate, exactement compensatrice pour toutes celles-ci. C'est ce qu'a fait Lorentz. Si nous désignons par V la vitesse de la lumière, par v la vitesse du mobile dans l'éther, Lorentz a trouvé que, pour qu'il y ait compensation dans tous les cas, il faut que la longueur du corps mobile soit raccourcie, dans le sens de sa marche, dans la proportion de 1 à 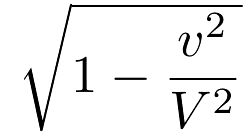. 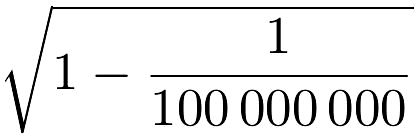Si à titre d'exemple nous prenons le cas de la translation terrestre où v = 30 kilomètres, on voit que la Terre est raccourcie suivant son orbite dans la proportion de ; la différence entre ces deux nombres est de 1/200 000 000, et la deux cent millionième partie du diamètre terrestre est égale à 6 centimètres et demi. C'est le nombre déjà trouvé.

Cette formule, qui donne la valeur de la contraction dans tous les cas, est élémentaire, et même pour un profane, la signification en est claire. Elle nous permet de calculer la valeur du raccourcissement pour [49] toute grandeur de la vitesse. On en déduit facilement que si la Terre avait une translation non plus de 30 kilomètres, mais de 260 000 kilomètres par seconde, elle serait raccourcie de moitié dans le sens de son déplacement (sans avoir ses dimensions altérées dans le sens perpendiculaire). A cette vitesse, une sphère devient un ellipsoïde aplati dont le petit axe égale la moitié du grand; à cette vitesse un carré devient un rectangle dont le côté parallèle au mouvement est deux fois plus petit que l'autre.

Ces déformations doivent apparaître à un observateur immobile; mais elles sont inappréciables à un observateur participant au mouvement, pour la raison que nous avons dite: les mètres et instruments de mesure et l'œil lui-même de cet observateur sont eux-mêmes et pareillement déformés.

Mettez-vous devant une de ces glaces étrangement bombées et déformantes qu'on voit dans certaines salles de spectacle; les unes vous montreront de vous-même une image extraordinairement allongée, sans que votre corpulence ait varié; d'autres au contraire vous montreront une image où vous aurez votre hauteur habituelle, mais où votre largeur multipliée sera grotesque. Essayez pourtant, avec un mètre gradué, de mesurer dans la glace et sur ces images déformées, votre hauteur et votre largeur. Si votre taille réelle est de 1 m. 70 et votre largeur réelle de 60 centimètres, le mètre juxtaposé à votre étrange image dans la glace vous indiquera toujours que cette image a 1 m. 70 [50] de hauteur et 60 centimètres de largeur. C'est que le mètre vu dans la glace a subi les mêmes déformations que l'image.

Cela fait que, même si le globe terrestre avait la vitesse fantastique dont nous avons parlé plus haut, les habitants de la Terre n'auraient aucun moyen de constater qu'elle et qu'eux-mêmes sont raccourcis de moitié dans le sens Est-Ouest. Un homme de 1 m. 70, couché et orienté du Nord au Sud dans un vaste lit carré, et à qui il prendrait fantaisie de se coucher ensuite en travers, orienté de l'Est à l'Ouest, n'aurait plus, à son insu, que 0 m. 85 de taille; en revanche sa corpulence aurait doublé dans le même temps, puisque tout à l'heure c'est elle qui était orientée de l'Est à l'Ouest. Mais la Terre ne se déplace que de 30 kilomètres par seconde, et sa déformation totale n'est, dans ces conditions, que de quelques centimètres.

A côté de cette vitesse de la Terre, celle de nos véhicules les plus rapides n'est que d'une faible fraction de kilomètre par seconde. Pour un avion faisant 360 kilomètres à l'heure, la vitesse n'est que de 100 mètres par seconde. La contraction Fitzgerald-Lorentz maxima de nos véhicules les plus rapides ne peut donc être que d'une fraction si infime de milliardième de millimètre qu'elle nous est complètement inappréciable. C'est pour cela, mais pour cela seulement, que la forme des objets solides qui nous sont familiers semble être invariable et constante, quelle que soit la vitesse à laquelle ils passent devant nos yeux. Il en serait tout autrement [51] si cette vitesse était des centaines de milliers de fois plus grande.

Tout cela est bien étrange, bien étonnant, bien fantastique, bien difficile à admettre. Et pourtant cela est, si la contraction Fitzgerald-Lorentz, seule explication possible—du moins jusqu'ici—de l'expérience de Michelson, existe réellement. Mais nous avons déjà vu quelques-unes des difficultés qu'il y a à concevoir l'existence de cette contraction.

Il en est d'autres. Si tout ce que nous venons de dire est vrai, les objets immobiles dans l'éther conserveraient seuls leur figure vraie; celle-ci serait déformée dès qu'il y a déplacement dans l'éther. Parmi les objets que nous voyons sphériques dans le monde extérieur (planètes, étoiles, projectiles, gouttes d'eau, que sais-je), il y en aurait donc qui sont réellement des sphères, tandis que d'autres, parce que leur mouvement est plus rapide ou plus lent, ne seraient que des ellipsoïdes allongés ou aplatis que la vitesse a déformés? Ainsi, parmi les divers objets carrés, il y en aurait qui seraient de vrais carrés, d'autres qui, animés de vitesses différentes par rapport à l'éther, ne seraient que des rectangles réels dont la vitesse a raccourci en apparence le plus long côté? Et nous n'aurions aucun moyen de savoir jamais quels sont, parmi ces objets animés de vitesses différentes, ceux dont nous voyons la vraie forme, ceux dont la forme n'est qu'apparente, puisque nous ne pouvons, l'expérience de Michelson le prouve, déceler une vitesse par rapport à l'éther?

[52] Non, non, et cent fois non, s'écrient les relativistes. Il y a dans tout cela trop de difficultés. Pourquoi parler sans cesse, comme fait Lorentz, de vitesses par rapport à l'éther puisque aucune expérience ne peut mettre en évidence une pareille vitesse et que l'expérience est la source unique de la vérité scientifique? Pourquoi d'autre part admettre que, parmi les objets sensibles, il en est de privilégiés qui, à l'exclusion des autres, se montrent sous leur aspect réel, sans déformation? Pourquoi admettre une chose pareille qui, en soi, répugne à l'esprit scientifique toujours ennemi des exceptions dans la nature,—il n'est de science que du général,—surtout quand ces exceptions sont indiscernables?

Les choses en étaient là,—fort avancées, au point de vue de l'expression mathématique des phénomènes, mais fort embrouillées, décevantes, contradictoires et choquantes même au point de vue physique—lorsque «enfin Malherbe vint»... je veux dire Einstein.

On ne peut aucunement mettre en évidence de telles vitesses, et il serait peut-être plus simple de ne plus faire intervenir dans tous les raisonnements cette chose, [54] réelle ou non, mais inaccessible et qui, dans la montée cahotante des physiciens à travers les ornières de ces difficultés, joue seulement le rôle inefficace et gênant de la cinquième roue du carrosse électromagnétique.

Premier point donc: Einstein provisoirement commence par laisser l'éther à l'écart de ses raisonnements; il ne nie, ni n'affirme sa réalité; il l'ignore d'abord.

C'est ce que nous allons maintenant faire à son exemple. Nous ne parlerons plus, dans notre démonstration, du milieu qui propage la lumière. Nous ne considérerons celle-ci que par rapport aux êtres ou objets matériels qui l'envoient ou la reçoivent. Du coup notre marche va se trouver singulièrement allégée. Pour l'éther des physiciens, nous le reléguerons un moment au magasin des accessoires inutiles, à côté de l'éther suave, amorphe et vague... mais si précieux prosodiquement, des poètes.

Que montre en somme l'expérience de Michelson? Qu'un rayon lumineux se propage à la surface de la terre de l'Ouest à l'Est exactement avec la même vitesse que de l'Est à l'Ouest. Imaginons au milieu d'une plaine deux canons identiques tirant, au même instant, par temps calme et sans vent, à la même vitesse initiale, deux projectiles semblables, l'un vers l'Ouest, l'autre vers l'Est. Il est clair que les deux projectiles mettront [55] le même temps pour franchir des espaces égaux, l'un vers l'Ouest, l'autre vers l'Est. Les rayons lumineux que nous pouvons produire sur la Terre se comportent à cet égard, dans leur propagation, exactement comme ces obus. Il n'y aurait donc rien d'étonnant au résultat de l'expérience de Michelson si nous ne connaissions, des rayons lumineux, que ce que nous enseigne cette expérience.

Mais poursuivons notre comparaison. Considérons l'obus tiré par un de ces canons, et supposons qu'il tombe sur un blindage, sur une cible, en un certain point du champ de tir, et qu'en parvenant à ce point la vitesse restante de l'obus soit par exemple 50 mètres par seconde. Supposons cette cible montée sur un tracteur automobile. Si celui-ci est arrêté, la vitesse de l'obus par rapport à la cible sera, nous venons de le dire, de 50 mètres par seconde au point d'impact. Mais je suppose que le tracteur et la cible qu'il porte soient lancés, par exemple, à la vitesse de 10 mètres à la seconde (cela fait du 36 kilomètres à l'heure) dans la direction du canon, de telle sorte que la cible passe à sa position précédente exactement à l'instant où l'obus lui arrive. Il est clair que la vitesse de l'obus par rapport à la cible au moment où il l'atteint, ne sera plus 50 mètres mais 50 + 10 = 60 mètres par seconde. Il est évident au contraire que cette vitesse ne serait plus, toutes choses égales d'ailleurs, que 50 − 10 = 40 mètres par seconde, si, au lieu d'être lancée vers le canon, la cible était lancée en sens inverse. Si la vitesse de la cible dans [56] ce dernier cas était égale à celle de l'obus, il est clair que celui-ci ne la toucherait plus qu'avec une vitesse nulle.

Tout cela va de soi-même, saute aux yeux. C'est pour cela que dans les music-halls les jongleurs peuvent recevoir sur une assiette, sans les casser, des œufs crus tombant de très haut: il leur suffit de donner à l'assiette, au moment du contact, une légère vitesse descendante qui amoindrit d'autant la vitesse du choc. C'est pour cela aussi, que les boxeurs habiles savent, par un léger mouvement, fuir devant le coup de poing, ce qui diminue sa vitesse efficace, tandis qu'au contraire, s'ils vont à sa rencontre, le coup est bien plus dur.

Si les rayons lumineux se comportaient en tout,—comme ils font dans l'expérience de Michelson—de même que nos projectiles, qu'arriverait-il? Lorsqu'on va très vite à la rencontre d'un rayon lumineux, on devrait trouver que ce rayon a, par rapport à l'observateur, une vitesse accrue, et qu'il a au contraire une vitesse diminuée lorsque l'observateur fuit devant lui. S'il en était ainsi, tout serait simple; les lois de l'optique seraient les mêmes que celles de la mécanique, aucune contradiction entre elles n'aurait jeté l'émoi dans l'armée paisible des physiciens, et Einstein aurait dû employer ailleurs les ressources de son génie.

Malheureusement,—ou peut-être heureusement, car, après tout, l'imprévu et le mystère seuls donnent du charme à la marche de ce monde,—il n'en est rien.

[57] Les observations physiques, comme les astronomiques, montrent qu'en toutes circonstances, qu'on coure très vite au-devant de la lumière ou qu'on fuie devant elle, toujours elle a, par rapport à l'observateur, exactement la même vitesse. Il y a, en particulier, dans le ciel des étoiles qui s'éloignent ou se rapprochent de nous, c'est-à-dire dont nous nous éloignons ou nous rapprochons avec des vitesses de plusieurs dizaines et même de centaines de kilomètres par seconde. Eh bien! l'astronome de Sitter a montré que la vitesse de la lumière qui nous en arrive est pour nous, et toujours, exactement la même.

Ainsi, on n'a jamais pu jusqu'ici, par aucun artifice, par aucun mouvement, ajouter ou retrancher quelque chose à la vitesse avec laquelle nous parvient un rayon lumineux. L'observateur constate que la propagation de la lumière est, par rapport à lui, toujours identique, que cette lumière provienne d'une source qui s'éloigne ou qui se rapproche très vite, qu'il se précipite à sa rencontre ou en sens contraire. L'observateur peut toujours augmenter ou diminuer la vitesse par rapport à lui d'un obus, d'une onde sonore, d'un mobile quelconque, en s'élançant vers ce mobile ou en fuyant devant lui. Quand le mobile est un rayon lumineux, on ne peut rien faire de pareil.

Ainsi, la vitesse d'un véhicule ne peut en aucun cas s'ajouter à celle de la lumière qu'il reçoit ou qu'il émet, ni s'en retrancher.

Cette vitesse-limite de près de 300 000 kilomètres [58] par seconde, qu'on observe toujours pour la lumière, est, à divers égards, analogue à la température de 273° au-dessous de zéro qu'on appelle le «zéro absolu» et qui est elle aussi, dans la nature, une limite infranchissable.

Tout cela prouve que les lois qui règlent les phénomènes optiques ne sont pas les mêmes que les lois classiques des phénomènes mécaniques. C'est à concilier, à réconcilier ces lois apparemment contradictoires que s'est attaché Lorentz, après Fitzgerald, par l'hypothèse étrange de la contraction.

Mais voici que, lumineusement, Einstein va nous montrer que cette contraction est une chose parfaitement naturelle lorsqu'on abandonne certaines conceptions peut-être erronées... encore que classiques, qui présidaient à notre manière habituelle, ancestrale, d'apprécier les longueurs et les temps.

Considérons un objet quelconque, une règle par exemple. Qu'est-ce qui définit pour nous la longueur apparente de cette règle? C'est l'image délimitée sur notre rétine par les deux rayons provenant des deux extrémités de la règle, et qui parviennent à notre pupille simultanément.

Je souligne à dessein ce mot, car il est ici la clef de tout. Si notre règle est immobile devant nous, cela est [59] tout simple. Mais si on la déplace pendant que nous la regardons, ce l'est moins. Ce l'est même si peu, qu'avant Einstein la plupart des plus grands savants et toute la science classique ont pensé que l'image instantanée d'un objet indéformable était nécessairement et toujours identique et indépendante des vitesses de l'objet et de l'observateur. C'est que toute la science classique raisonnait comme si la propagation de la lumière avait été elle-même instantanée, avait eu une vitesse infinie, ce qui n'est pas.

Je suis sur le talus, au bord d'une ligne de chemin de fer; sur la voie il y a un de ces beaux wagons allongés de la Compagnie des wagons-lits, où il est si agréable de penser que l'espace est relatif, au sens galiléen du mot. Je fais planter tout au bord de la voie deux piquets l'un bleu, l'autre rouge, qui marquent exactement les extrémités de ce wagon et qui encadrent tout juste sa longueur. Puis, sans quitter mon poste d'observation qui est sur le talus, face au milieu du wagon, j'ordonne que celui-ci soit ramené en arrière et attelé à une locomotive d'une puissance inouïe qui va le faire passer devant moi à une vitesse fantastique, dépassant des millions de fois toutes celles qu'ont pu réaliser les ingénieurs... tant est grande la supériorité potentielle de l'imagination sur la médiocre réalité. Je suppose aussi que ma rétine est parfaite et constituée de telle sorte que les impressions visuelles n'y durent qu'autant que la lumière qui les provoque.

Ces hypothèses un peu arbitraires n'entrent pour rien [60] dans le fond de la démonstration; elles la rendent seulement plus commode.

Et maintenant voici la question. Quand le wagon-lit, que je suppose fait, d'ailleurs, d'un métal indéformable, passera à toute vitesse devant moi, aura-t-il pour moi exactement la même longueur apparente que lorsqu'il était au repos? Autrement dit, à l'instant où je verrai son extrémité avant coïncider en passant avec le piquet bleu que j'ai fait planter, verrai-je son extrémité arrière coïncider en même temps avec le piquet rouge? A cette question, Galilée, Newton et tous les tenants de la science classique auraient répondu oui. Et pourtant la réponse est non selon Einstein.

En voici la démonstration très simple et telle qu'elle dérive de la conception einsteinienne.

Je suis, rappelons-le, placé au bord de la voie, à égale distance des deux piquets. Lorsque l'extrémité antérieure du wagon coïncide avec le piquet bleu, elle envoie vers mon œil un certain rayon lumineux (que j'appelle pour simplifier rayon-avant) qui coïncide avec le rayon que m'envoie le piquet bleu. Ce rayon-avant atteint mon œil en même temps qu'un certain rayon venu de l'extrémité arrière du wagon (et que j'appelle pour simplifier rayon-arrière). Le rayon-arrière coïncide-t-il avec le rayon que m'envoie le piquet rouge? Évidemment non: en effet le rayon-avant s'éloigne de l'extrémité avant du wagon avec la même vitesse que le rayon-arrière de l'extrémité arrière (comme le constaterait un voyageur qui, dans le wagon, ferait sur ces rayons [61] l'expérience de Michelson). Mais l'extrémité avant du wagon s'éloigne de mon œil tandis que l'extrémité arrière s'en approche. Par conséquent le rayon-avant se propage vers mon œil plus lentement que le rayon-arrière, sans que je puisse d'ailleurs m'en apercevoir, puisque à leur arrivée je trouve la même vitesse aux deux rayons. Par conséquent le rayon-arrière qui arrive à mon œil en même temps que ledit rayon-avant, a dû quitter l'extrémité arrière du wagon plus tard que le rayon-avant n'a quitté son extrémité avant. Donc lorsque je vois le bord antérieur du wagon coïncider avec le piquet bleu, je vois simultanément le bord arrière du wagon qui a déjà dépassé depuis un certain temps le piquet rouge.

Donc la longueur du wagon lancé à toute vitesse, et telle qu'elle m'apparaît, est plus petite que la distance des deux piquets, laquelle marquait la longueur du wagon au repos. (C. Q. F. D.).

Avec un peu d'attention, tout le monde comprendra cette démonstration dont la simplicité élémentaire n'a point été obtenue sans peine, mais qui se ramène en fait à la démonstration mathématique d'Einstein et à sa conception de la simultanéité.

Il en résulte que le wagon ou, d'une manière générale, un objet quelconque semble raccourci par sa vitesse et dans le sens de celle-ci par rapport à l'observateur. [62] La même chose a lieu évidemment si c'est l'observateur qui se déplace devant l'objet, puisqu'on ne peut connaître que des vitesses relatives, en vertu du principe de relativité classique de Newton et de Galilée.

Sous cet aspect nouveau, la contraction de Lorentz-Fitzgerald devient intelligible ou du moins admissible. Cette contraction n'est plus, de la sorte, la cause du résultat négatif de l'expérience de Michelson; elle en est la conséquence. Tout s'en trouve clarifié, et on comprend maintenant qu'il y avait, dans la façon classique d'évaluer la dimension instantanée des objets, quelque chose d'incorrect.

Certes, le fait que des rayons lumineux, animés de vitesses différentes au départ de leurs sources, aient toujours en arrivant à notre œil des vitesses identiques et indiscernables, est étrange et heurte quelque peu nos vieilles habitudes d'esprit. Si j'ose employer une comparaison qui est seulement destinée à faire penser, mais nullement à expliquer, il y a là peut-être quelque chose d'analogue à ce qui se passe avec les bombes d'avions. Des bombes d'un modèle donné, qu'elles soient lâchées par l'avion d'une hauteur de 5 000 mètres ou d'une hauteur de 10 000, et qui, par conséquent, ont à 5 000 mètres du sol des vitesses de chute fort dissemblables, ont toujours en arrivant au sol la même vitesse restante. C'est l'effet modérateur, égalisateur, de la résistance de l'air, qui empêche la vitesse de s'accroître indéfiniment et la rend constante lorsqu'elle atteint une certaine valeur.

[63] Faut-il admettre qu'autour de notre œil, autour des objets, il y a une sorte de champ de résistance qui impose à la lumière survenante une limite semblable? Qui le sait? D'ailleurs ces questions n'ont peut-être pas de sens pour un physicien. Celui-ci ne peut connaître et ne connaîtra le comportement de la lumière qu'à son départ de la source matérielle et à son arrivée à l'œil armé ou non d'instruments. Il ne peut savoir comment se comporte sa propagation dans l'espace intermédiaire dénué de matière.

Plus d'ailleurs nous approfondirons la nouvelle physique, plus nous constaterons qu'elle puise presque toute sa force dans son dédain systématique de ce qui n'est pas phénoménal, de ce qui n'est pas expérimentalement observable. C'est parce qu'elle est basée uniquement sur les faits (si contradictoires soient-ils) que notre démonstration du raccourcissement nécessaire des objets par leur vitesse relative à l'observateur, est forte.

Nous comprenons maintenant le sens profond de la contraction de Fitzgerald-Lorentz. Cette contraction apparente n'est nullement due au mouvement des objets par rapport à l'éther; elle est essentiellement l'effet des mouvements des objets et des observateurs les uns par rapport aux autres, des mouvements relatifs, au sens de la vieille mécanique.

[64] Les plus grandes vitesses relatives auxquelles nous soyons habitués, dans la pratique de l'existence, sont inférieures à quelques kilomètres par seconde. La vitesse initiale de l'obus de la Bertha n'était que d'environ 1 300 mètres par seconde. Pour des mouvements aussi lents, la contraction relativiste est complètement négligeable. C'est pourquoi, ne l'ayant jamais constatée, la mécanique classique a considéré la forme et la dimension des objets rigides comme indépendantes des systèmes de référence.

C'était à peu près vrai. C'est là toute la différence qu'il y a entre le vrai et le faux. Dire que 999 990 + 9 = 1 million, c'est dire quelque chose d'à peu près vrai, donc de faux. Quand la rotondité de la Terre fut démontrée, elle ne changea assurément rien aux procédés des architectes, qui construisent encore leurs bâtisses comme si la direction marquée par le fil à plomb était toujours parallèle à elle-même. Pareillement, nos fabricants de locomotives et d'avions n'auront pas de longtemps à considérer les formes de leurs machines comme dépendant de leurs vitesses. Qu'importe! Le point de vue de la pratique n'est et ne doit être celui de la science que par ricochet. Tant pis s'il n'y a pas de ricochet, ou s'il est tardif.

D'ailleurs, on a découvert depuis quelques années, ici-bas, des mobiles dont les vitesses, relatives à nous, atteignent des dizaines, des centaines de milliers de kilomètres: ce sont les projectiles des rayons cathodiques et des rayons du radium. A ces allures, la contraction [65] relativiste est très notable. Nous verrons comment, effectivement, elle a été notée.

Récapitulons ce qui est maintenant acquis:

Les objets apparaissent déformés dans le sens de leur mouvement et non dans le sens perpendiculaire. Donc leur forme, fussent-ils d'une matière idéale et parfaitement indéformable, dépend de leur vitesse rapportée à l'observateur. Ceci est le point de vue essentiellement neuf que la «relativité spéciale» d'Einstein surajoute à la relativité des mécaniciens classiques, et à la relativité des philosophes. Pour eux, les dimensions absolues d'un objet rigide ou d'une figure géométrique n'avaient rien d'absolu, et seuls les rapports de ces dimensions avaient une réalité.

Le point de vue nouveau est que ces rapports eux-mêmes sont relatifs, puisqu'ils sont fonction de la vitesse de l'observateur. C'est une sorte de relativité au second degré, à laquelle les philosophes, ni les physiciens classiques n'avaient songé.

Les relations spatiales elles-mêmes sont relatives, dans un espace déjà relatif.

Dans le cas de notre wagon de tout à l'heure et des deux piquets qui définissent sa longueur au repos, un observateur placé dans le wagon trouverait que la distance des deux piquets s'est raccourcie lorsqu'il les croise. Son wagon lui semble plus long que l'intervalle des piquets. Moi qui demeure entre ceux-ci, je constate le contraire. Et pourtant je n'ai aucun moyen de démontrer au voyageur qu'il s'est trompé. Je vois [66] très bien que le rayon lumineux venu du piquet arrière court derrière le wagon et par conséquent a, par rapport à lui, une vitesse inférieure à 300 000 kilomètres par seconde; je sais que de là provient l'erreur du voyageur, mais je n'ai aucun moyen de le convaincre de cette erreur, car il me répondra toujours et avec raison: «J'ai mesuré la vitesse avec laquelle ce rayon m'arrive et je l'ai trouvée égale à 300 000 kilomètres.» Chacun de nous en réalité a raison.

En mouvement très rapide, un carré paraîtrait un rectangle à l'observateur; un cercle paraîtrait elliptique. Si la Terre tournait quelques milliers de fois plus vite autour du Soleil, nous le verrions allongé et pareil à un gigantesque citron suspendu dans le ciel. Si un aviateur pouvait survoler à une vitesse fantastique la place Vendôme, suivant la direction de la rue de la Paix,—et si ses impressions rétiniennes étaient instantanées,—la place aurait pour lui la forme d'un rectangle très aplati; s'il la survolait suivant une diagonale, il la verrait, de carrée qu'elle était, devenir un losange. Si le même aviateur survolait, en la coupant, une route où chemine du bétail bien engraissé conduit vers l'abattoir, il s'étonnerait, car les animaux lui sembleraient étonnamment minces et maigres sans que leur longueur ait varié.

Le fait que les déformations dues à la vitesse sont réciproques est une des conséquences les plus curieuses de tout cela. Un homme qui serait capable de circuler en tous sens parmi les autres hommes avec la vitesse [67] fantastique des follets shakespeariens (mettons à environ 260 000 kilomètres à la seconde... mais que ne peut un follet shakespearien!) trouverait que ses semblables sont devenus des nains deux fois plus petits que lui. C'est donc que lui-même serait devenu un géant, une sorte de Gulliver parmi ces Lilliputiens? Eh bien! pas du tout. Par un juste retour des choses d'ici-bas, il apparaîtrait lui aussi comme un nain à ceux qu'il croit plus petits que lui, et qui sont sûrs du contraire.

Qui a raison, qui a tort? Les uns et les autres. Tous les points de vue sont exacts, mais il n'y a que des points de vue personnels.

Autre chose encore: un observateur, quel qu'il soit, ne peut voir les êtres et les objets non liés à lui que plus petits,—jamais plus grands!—que ceux liés à son mouvement. Si j'osais alléger ce grave exposé par quelque réflexion moins austère qu'il n'est d'usage parmi les physiciens, je remarquerais que le système nouveau nous apporte ainsi une justification suprême de l'égoïsme ou plutôt de l'égocentrisme.

Après l'espace, le temps. Par un raisonnement analogue à celui qui nous a montré la distance des choses dans l'espace liée à leur vitesse relative à l'observateur, on peut établir que leur distance dans le temps en dépend également.

Je ne juge pas utile de refaire ici, par le menu, le raisonnement einsteinien pour les durées; il serait analogue à celui qui nous a servi pour les longueurs, et encore plus simple. Le résultat est le suivant: le temps [68] exprimé en secondes que met un train à passer d'une station à une autre est plus court pour les voyageurs du train que pour nous qui les regardons passer, et qui sommes munis d'ailleurs de chronomètres identiques aux leurs[4]. Pareillement tous les gestes faits par des hommes, sur un véhicule en mouvement, apparaîtront ralentis et par conséquent prolongés à un observateur immobile, et réciproquement. Pour que ces variations des durées fussent sensibles, il faudrait, comme pour les variations concomitantes des longueurs, que les vitesses fussent fantastiques.

Il n'en est pas moins vrai que la durée qui sépare la naissance et la mort d'une créature quelconque, c'est-à-dire sa vie, paraîtra prolongée si cette créature se déplace très vite et frénétiquement par rapport au regardant. Dans ce monde où paraître est presque tout, cela a bien son importance, et il reste de tout cela que, philosophiquement parlant, se mouvoir c'est durer davantage... pour les autres, non pour soi; c'est aussi voir durer davantage les autres.

Admirable justification, et combien profonde et imprévue, de ce que le sage avait entrevu: l'immobilité, c'est la mort.

[69]

Naguère, avant l'hégire einsteinienne, avant le début de l'ère relativiste, chacun était persuadé que la portion de l'espace occupée par un objet était suffisamment et explicitement définie par ses dimensions dans le sens de la longueur, de la largeur, de la hauteur. Ces données sont ce qu'on appelle les trois dimensions d'un objet; comme encore, si on préfère employer d'autres points de repères, la longitude, la latitude et l'altitude de chacun de ses points; ou bien, en astronomie, l'ascension droite, la déclinaison et la distance.

Il était bien entendu et bien connu qu'en outre il fallait préciser l'époque, l'instant auquel correspondaient ces données. Si je définis la position d'un aéronef par sa longitude, sa latitude et son altitude, ces indications ne sont exactes que pour l'instant considéré, puisque l'aéronef se déplace par rapport au repère,—et cet instant doit être donné lui aussi. En ce sens, on sentait depuis longtemps que l'espace dépend du temps.

Mais la théorie relativiste montre qu'il en dépend d'une manière bien plus intime encore et bien plus profonde, et que le temps et l'espace sont aussi liés et solidaires que ces monstres xiphopages que les chirurgiens ne peuvent séparer sans tuer l'un et l'autre.

Les dimensions d'un objet, sa forme, l'espace apparent occupé par lui dépendent de sa vitesse, c'est-à-dire du temps que met l'observateur à parcourir une certaine [70] distance par rapport à cet objet. A cet égard déjà, l'espace dépend du temps; en outre, l'observateur mesure ce temps avec un chronomètre dont les secondes sont plus ou moins précipitées selon cette vitesse.

Donc définir l'espace sans le temps est impossible. C'est pourquoi on dit maintenant que le temps est la quatrième dimension de l'espace, et que l'espace où nous vivons a quatre dimensions.

Il est curieux que certains bons esprits, dans le passé, en avaient eu l'intuition plus ou moins obscure. C'est ainsi qu'en 1777 Diderot écrivait dans l'Encyclopédie à l'article «Dimension»:

«... J'ai dit plus haut qu'il était impossible de concevoir plus de trois dimensions. Un homme d'esprit de ma connaissance croit qu'on pourrait cependant regarder la durée comme une quatrième dimension et que le produit du temps par la solidité serait, en quelque manière, un produit de quatre dimensions. Cette idée peut être contestée, mais elle a, il me semble, quelque mérite, quand ce ne serait que celui de la nouveauté.»

C'est à coup sûr de l'algèbre qu'est née la première idée d'un espace à plus de trois dimensions. Puisqu'en effet les lignes ou espaces à une dimension sont représentés par des expressions algébriques du premier degré, les surfaces ou espaces à deux dimensions par des formules du second degré, les volumes ou espaces à trois dimensions par des expressions du troisième degré, il était naturel de se demander si les formules du quatrième degré et au delà ne sont pas, elles [71] aussi, la représentation algébrique de quelque forme d'espace à quatre dimensions et davantage.

L'espace à quatre dimensions des relativistes n'est, au surplus, pas tout à fait ce qu'imaginait Diderot. Il n'est pas le produit du temps par l'étendue, car une diminution du temps n'y est pas compensée par un accroissement de l'espace, bien au contraire.

Considérons deux événements, par exemple les passages successifs, de notre rapide wagon-lit à deux stations. Pour un voyageur du wagon la distance des deux stations, mesurée par la longueur du chemin parcouru, est, comme nous l'avons montré, plus courte que pour un observateur immobile au bord de la voie. Le temps qui sépare les deux passages est également moindre pour le premier observateur. En effet le nombre des secondes et fractions de secondes écoulées au chronomètre dont il est muni, est plus petit pour lui, nous l'avons vu.

En un mot, la distance dans le temps et la distance dans l'espace diminuent toutes deux en même temps lorsque la vitesse de l'observateur augmente et augmentent toutes deux quand la vitesse de l'observateur diminue.

Ainsi la vitesse (et il ne s'agit jamais, rappelons-le, que de la vitesse relativement aux choses observées), opère en quelque sorte comme un double frein qui ralentit les durées et raccourcit les longueurs. Si l'on préfère une autre image, la vitesse nous fait voir à la fois les espaces et les temps plus obliquement, sous un [72] angle de plus en plus aigu. L'espace et le temps ne sont donc que des effets changeants de perspective.

Pouvons-nous concevoir l'espace à quatre dimensions, c'est-à-dire pouvons-nous en imaginer une représentation sensible? Si non, cela ne prouvera rien contre la réalité de cet espace. Pendant des siècles on n'a pas conçu les ondes hertziennes et aujourd'hui encore elles ne nous sont pas directement sensibles. En existent-elles moins? En vérité, nous ne concevons déjà que difficilement l'espace à trois dimensions. Sans nos déplacements musculaires nous l'ignorerions. Un homme paralysé et borgne, c'est-à-dire n'ayant pas la sensation du relief que donne la vision binoculaire,—qui est, elle aussi, avant tout, un tâtonnement musculaire,—verrait de son œil unique et immobile tous les objets projetés dans un même plan, comme sur une toile de fond au théâtre. L'espace à trois dimensions lui serait inaccessible.

Je crois que certaines personnes peuvent se représenter l'espace à quatre dimensions. Les aspects successifs d'une fleur aux différents âges de sa croissance, du jour où elle n'est qu'un fragile bourgeon vert jusqu'à celui où ses pétales épuisés tombent dolents, et les divers déplacements successifs de sa corolle sous l'influence du vent constituent une image globale de la fleur dans l'espace à quatre dimensions.

Est-il des hommes pouvant d'un seul coup voir tout cet ensemble? Oui, et notamment, je crois, les bons joueurs d'échecs. Si un grand joueur d'échec joue bien, [73] c'est parce que, d'un seul regard de son œil mental, il embrasse l'ensemble chronologique et spatial des coups possibles dérivés d'un seul coup initial, avec toutes leurs répercussions sur l'échiquier. Il en voit simultanément toute la succession.

Ces mots soulignés jurent un peu d'être accouplés. C'est que nous sommes dans un domaine où prétendre exprimer vocabulairement les nuances des choses est une gageure. Autant vaudrait, après tout, tenter de définir avec des mots tout ce qu'il y a dans une symphonie de Beethoven. «Traduttore traditore»: si cet adage est vrai, c'est surtout parce que le mot est l'organe de la traduction.

Arrivés à ce point, dans notre lente ascension de la physique relativiste, nous n'avons plus devant les yeux qu'un champ de bataille où gisent des cadavres et des débris.

Le temps et l'espace, nous croyions ces crochets solidement rivés au mur derrière lequel se cache la réalité, et nous y attachions nos flottantes notions du monde extérieur, ainsi que des vêtements à des portemanteaux. Ils gisent maintenant arrachés et tordus dans le plâtras des anciennes théories, sous les coups de marteau de la physique nouvelle.

Nous savions bien, certes, que l'âme des êtres nous [74] était cachée, mais nous pensions du moins voir leur visage. Voilà qu'en nous approchant, celui-ci n'est plus qu'un masque. Le monde extérieur, que nous montre Einstein, n'est rien qu'un bal travesti, et par une ironie décevante, c'est nous-mêmes qui avons fabriqué les loups de velours aux reflets changeants, les costumes papillotants.

Loin de nous révéler la réalité, l'espace et le temps ne sont, selon Einstein, que des voiles mouvants, tissés par nous-mêmes, et qui la cachent à nos yeux. Et pourtant, chose étrange et mélancolique, nous ne pouvons pas plus concevoir le monde sans le temps et l'espace que nous ne pouvons observer certains microbes au microscope sans les injecter de matières colorantes.

Le temps et l'espace ne sont-ils donc que des hallucinations? Et alors, que reste-t-il?

Eh bien! non. Car voici qu'après avoir détruit les ruines branlantes, la doctrine relativiste va soudain reconstruire. Voici que, derrière les voiles déchirés et foulés aux pieds, va surgir une réalité plus neuve, plus subtile.

Si nous décrivons l'univers à la manière habituelle, séparément dans les catégories du temps et de l'espace, nous voyons que son aspect dépend de l'observateur. Il n'en est heureusement pas de même lorsqu'on le décrit dans la catégorie unique de ce continuum à quatre dimensions où Einstein situe les phénomènes et où le temps et l'espace unis sont étroitement solidaires.

[75] Si j'ose employer cette image, le temps et l'espace sont comme deux miroirs, l'un convexe, l'autre concave,—dont les courbures sont d'autant plus accusées que la vitesse de l'observateur est plus grande. Chacun de ces deux miroirs donne séparément une image déformée de la succession des choses. Mais, par une heureuse compensation, il se trouve qu'en combinant les deux miroirs de telle sorte que l'un réfléchisse les rayons reçus par l'autre, l'image de cette succession est rétablie dans sa réalité non déformée.

La distance dans le temps et la distance dans l'espace de deux événements donnés très voisins augmentent toutes deux ou diminuent toutes deux quand la vitesse de l'observateur diminue ou augmente. Nous l'avons établi. Mais le calcul qui est facile, grâce à la formule donnée ci-dessus pour exprimer la contraction de Lorentz-Fitzgerald, montre qu'il existe une relation constante entre ces variations concomitantes du temps et de l'espace. Pour préciser, la distance dans le temps et la distance dans l'espace de deux événements voisins sont numériquement entre elles comme l'hypoténuse et un autre côté d'un triangle rectangle sont au troisième côté lequel resterait invariable[5].

Ce troisième côté étant pris pour base, les deux autres dessineront, au-dessus de lui, un triangle plus ou moins haut, selon que la vitesse de l'observateur sera plus [76] ou moins réduite. Cette base fixe du triangle dont les deux autres côtés,—la distance spatiale et la distance chronologique,—varient simultanément avec la vitesse de l'observateur, est donc une quantité indépendante de cette vitesse.

C'est cette quantité, qu'Einstein a appelée l'intervalle des événements. Cet «intervalle» des choses dans l'espace-temps à quatre dimensions est une sorte de conglomérat de l'espace et du temps, un amalgame de l'un et de l'autre dont les composants peuvent varier, mais qui, lui, reste invariable. Il est la résultante constante de deux vecteurs changeants. L'«intervalle» des événements, ainsi défini, nous fournit pour la première fois, selon la physique relativiste, une représentation impersonnelle de l'Univers.

Suivant la saisissante image de Minkowski, «l'espace et le temps ne sont que des fantômes. Seul existe dans la réalité une sorte d'union intime de ces deux entités.»

L'unique réalité saisissable à l'homme dans le monde extérieur, la seule donnée vraiment objective et impersonnelle qui nous soit accessible, c'est donc l'Intervalle einsteinien, tel qu'il vient d'être défini. L'Intervalle des événements est pour les relativistes la seule part sensible du réel. Hors de là, il y a peut-être quelque chose, mais rien que nous puissions connaître.

Étrange destinée de la pensée humaine! Le principe de relativité, par les découvertes de la physique moderne, a étendu son aile vaporeuse bien plus loin qu'autrefois et jusqu'à des sommets qu'on croyait inaccessibles à [77] son vol aquilin. Et c'est à lui pourtant que nous devons peut-être la première emprise véritable de notre faiblesse sur le monde sensible, sur la réalité.

Le système d'Einstein, dont il nous reste à voir maintenant la partie constructive, disparaîtra un jour comme les autres. Il n'existe dans la science que des théories «à titre temporaire», jamais de théories «à titre définitif»... et c'est peut-être ce qui a multiplié ses victoires. La notion de l'Intervalle des choses survivra sans doute à tous les écroulements. Sur elle devra être bâtie la science de l'avenir; sur elle s'élève chaque jour l'édifice hardi de la science d'aujourd'hui.

Encore ceci doit-il être formellement entendu: l'Intervalle einsteinien ne nous apprend rien sur l'absolu, sur les choses en soi. Il ne nous indique, lui aussi, que des rapports entre ces choses. Mais les relations qu'il manifeste semblent être véritables et invariantes.

Elles participent de ce degré de vérité objective que la science classique attribuait, avec une assurance peut-être fallacieuse, aux relations chronologiques et aux relations spatiales des phénomènes. Aux yeux de la physique nouvelle celles-ci n'étaient que des balances fausses, et seul l'Intervalle einsteinien nous livre ce qui peut être connu du Réel.

Ainsi la doctrine d'Einstein s'enorgueillit d'avoir levé à jamais un coin du voile décevant qui nous dérobe la nudité sacrée de la Nature.

Le mouvement déforme donc les lignes bien plus que ne pensait Baudelaire, et même celles des plus marmoréennes statues. Cette déformation-là, qu'il faut aimer [79] et non haïr, parce qu'elle nous rapproche du cœur même des choses, a bouleversé d'abord la mécanique entière.

La mécanique est à la base de toutes les sciences expérimentales parce qu'elle est la plus simple et parce que les phénomènes qu'elle étudie sont toujours présents,—sinon exclusivement présents,—parmi les phénomènes objets des autres sciences plus complexes, physique, chimie, biologie. La réciproque n'est pas vraie.

Par exemple, il n'y a pas un seul phénomène chimique ou biologique où l'on ne doive considérer des corps qui sont en mouvement, qui ont une masse, qui dégagent ou absorbent de l'énergie.

Au contraire, les particularités d'un phénomène biologique, chimique, ou physique, par exemple l'existence d'une différence de potentiel, ou d'une oxydation, ou d'une pression osmotique ne se retrouvent pas toujours dans l'étude des mouvements d'une masse pesante et des forces agissant sur elle et par elle.

Par rapport à la mécanique, la physique, la chimie, la biologie ont, rangés dans cet ordre, des objets de complexité croissante et de généralité, ou, pour mieux dire, d'universalité décroissante. Ces sciences ont une dépendance réciproque qui est celle du tronc d'un arbre avec ses branches, ses rameaux et ses fleurs. Elles sont aussi entre elles un peu comme les pièces emboîtées des mâts où les télégraphistes militaires fixent leurs antennes. La pièce inférieure du mât, plus large, soutient le tout, mais ce sont les pièces supérieures qui portent les organes délicats et compliqués.

[80] L'objet des grands synthétistes de la science a toujours été et est encore de ramener, comme l'avait tenté Descartes, tous les phénomènes aux phénomènes mécaniques. Que ces tentatives soient ou non fondées, qu'elles puissent un jour aboutir ou qu'elles soient, au contraire, a priori vouées à l'échec parce que les phénomènes physico-biologiques contiennent peut-être des éléments essentiellement irréductibles aux éléments mécaniques, c'est une question qui a été et qui sera encore très disputée. Mais quelles que soient à cet égard les attitudes variées des penseurs, ils sont d'accord sur ceci: dans tous les phénomènes naturels, dans tous les phénomènes objets de science, il y a l'élément mécanique,—pour les uns élément exclusif, pour les autres élément principal, mais seulement partiel, des réalités objectives.

Si je rappelle ici tout cela, c'est pour en arriver à cette conclusion: tout ce qui modifie la mécanique, modifie du même coup l'édifice des notions fondées sur elle, c'est-à-dire les autres sciences, toute la science, et notre conception de l'Univers.

Or nous allons voir que la théorie d'Einstein, par une conséquence immédiate de ce qu'elle nous a enseigné déjà du temps et de l'espace, bouleverse de fond en comble la mécanique classique. C'est pour cela, et par cela surtout, qu'elle a porté dans l'édifice un peu somnolent de la science traditionnelle un ébranlement dont les vibrations ne sont pas près de cesser.

En abordant la mécanique einsteinienne, nous aurons [81] la joie de passer des conceptions un peu trop exclusivement géométriques et psychologiques de temps et d'espace, à l'étude directe des réalités sensibles, des corps. Ici nous pourrons confronter la théorie et la réalité, les prémisses mathématiques et les vérifications substantielles, et nous aurons le plaisir de voir par les faits, par l'expérience, ce qu'il faut penser de tout cela. Entre les anciennes manières de concevoir et la nouvelle, nous pourrons choisir en connaissance de cause, d'après des critères visibles.

En un mot, et si j'ose employer cette image, tant qu'il s'agissait des notions d'espace et de temps, cadres assez vides par eux-mêmes, vases intéressants surtout par les liquides qu'ils contiennent, nous étions un peu comme ces jeunes gens qui doivent choisir une fiancée d'après les seules descriptions qu'on leur a faites. Nous allons voir maintenant de nos propres yeux, et à l'œuvre, les deux prétendantes à notre dilection: la science classique et la théorie d'Einstein. Nous les verrons toutes deux mettre la main à la pâte des faits, et nous pourrons comparer les mets délectables qu'elles en auront respectivement tirés pour la nourriture de notre esprit.

Les théories ne valent qu'en fonction des faits, et celles qui, comme tant de métaphysiques, ne trouvent point de critère réel pour les départager, valent toutes également. L'expérience, source unique du savoir et dont Lucrèce disait déjà

[82] les faits sensibles, voilà ce qui va juger le système einsteinien.

Le résultat de l'expérience de Michelson, l'impossibilité de mettre en évidence aucune vitesse de la Terre par rapport au milieu dans lequel se propage la lumière, ce fait, avons-nous dit déjà, revient à ceci: on ne peut par aucun moyen constater, réaliser une vitesse supérieure à celle de la lumière. Cette conséquence de l'expérience de Michelson gagnera peut-être à être déduite sous une forme tangible. Voici une image qui y pourvoit.

Dans je ne sais plus quel roman astronomique, un observateur imaginaire est supposé s'éloigner de la Terre avec une vitesse supérieure à celle de la lumière, 500 000 kilomètres à la seconde, par exemple, tout en maintenant ses yeux (munis au besoin de puissantes besicles) constamment dirigés vers ce petit globe fébrile.

Que va-t-il arriver? Notre observateur verra évidemment les phénomènes terrestres à l'envers, puisque, dans son voyage, il rattrapera successivement des ondes lumineuses qui ont quitté la terre avant lui, et depuis d'autant plus longtemps qu'elles en sont plus éloignées. Notre homme, ou plutôt notre surhomme, assistera donc au bout d'un certain temps à la bataille de la Marne. Il verra d'abord le champ de bataille [83] couvert de morts. Petit à petit ces morts se relèveront pour rejoindre leur poste de combat et finalement ils se rangeront par escouades dans les taxis de Gallieni, lesquels regagneront Paris à toute vitesse et en marche-arrière, arrivant au milieu de la population inquiète de l'issue du combat dont nos soldats ne pourront, et pour cause, apporter nulle nouvelle. En un mot, notre observateur, s'il s'éloigne de la Terre avec une vitesse supérieure à celle de la lumière, verra les événements terrestres se dérouler en remontant le cours du temps.

Mais les choses se passeront très différemment si, au contraire, notre observateur restant immobile, c'est la Terre qui s'éloigne de lui avec une vitesse de 500 000 kilomètres à la seconde. Qu'arrivera-t-il alors? Il est clair qu'en ce cas notre observateur verra les événements terrestres non plus à l'envers mais à l'endroit. Il y a cette différence toutefois, qu'ils lui paraîtront se dérouler avec une majestueuse lenteur, puisque les rayons lumineux ayant quitté la Terre à la fin d'un événement quelconque, mettront beaucoup plus de temps à lui parvenir que les rayons qui ont quitté la Terre au commencement.

En résumé, les phénomènes observés par lui étant essentiellement différents dans les deux cas, notre observateur supposé aurait un moyen de savoir si c'est lui qui s'éloigne de la Terre ou si c'est la Terre qui s'éloigne de lui, de déceler la translation vraie de la Terre dans l'espace. Translation par rapport au milieu qui propage [84] la lumière... ce qui ne veut pas nécessairement dire,—nous l'avons montré,—translation par rapport à l'espace absolu.

L'expérience telle que nous venons de la concevoir ne serait pas facile à réaliser avec les ressources actuelles de nos laboratoires. Nous ne pouvons pas obtenir des vitesses aussi fantastiques, et, si nous les obtenions, l'observateur ne distinguerait pas grand'chose. Mais nous avons pris un exemple énorme et les résultats en auraient été énormes, puisqu'il ne s'agissait de rien moins que de renverser l'ordre des temps.

Supposons que nous employions des moyens plus modestes, les résultats seront plus modestes, mais ils devraient, d'après les anciennes théories, être encore appréciables pour nos instruments. Or l'expérience de Michelson,—qui serait en plus petit celle que nous venons de décrire,—montre que les différences attendues ne sont pas observées. Donc les prémisses que nous avons posées, à savoir qu'il peut exister des vitesses supérieures à celle de la lumière dans le vide, ne correspondent pas à la réalité. Donc cette vitesse est un mur, une limite qui ne peut être dépassée.

Voyons les conséquences. Il y a à la base de la mécanique classique, telle que l'ont fondée Galilée, Huyghens, Newton, telle qu'on l'enseigne partout, un principe [85] fondé en dernière analyse, comme tous ceux de la mécanique, sur l'expérience. C'est le principe de la composition des vitesses. Si un navire fait en eau calme du 10 kilomètres à l'heure et qu'il descende un fleuve dont la vitesse est de 5 kilomètres à l'heure, la vitesse du navire par rapport au rivage immobile sera, comme on peut le mesurer et le constater, égale à la somme de ces deux vitesses, c'est-à-dire à 15 kilomètres à l'heure. C'est la règle de l'addition des vitesses.

D'une manière plus générale, si un corps part du repos et sous l'action d'une force prend en une seconde une vitesse V, que va-t-il faire, si l'action de la force se prolonge pendant une deuxième seconde? Il prendra, d'après la mécanique classique, une vitesse 2V[6]. Supposons, en effet, un observateur animé d'une vitesse de translation V et qui se croit au repos. Pour lui, à la fin de la première seconde le corps paraît au repos (puisqu'il a la même vitesse que l'observateur). En vertu du principe de relativité classique, le mouvement apparent de ce corps doit être le même pour notre observateur que si ce repos était réel. C'est-à-dire qu'à la fin de la deuxième seconde, la vitesse relative du corps par rapport à l'observateur sera V, [86] et comme l'observateur a déjà une vitesse V, la vitesse absolue du corps sera 2V. On verrait de même qu'elle serait 3V au bout de trois secondes, 4V au bout de 4 secondes et ainsi de suite. Elle pourrait donc croître au delà de toute limite, si la force agit pendant assez longtemps? Oui, dit la mécanique classique. Non, dit Einstein, puisque aucune vitesse ne peut dépasser celle de la lumière dans le vide.

Nous avons supposé un observateur qui possède la vitesse V par rapport à nous et qui se croit au repos. Pour lui, le corps observé était également au repos au début de la deuxième seconde, puisque sa vitesse était la même que celle de l'observateur. De ce que le mouvement apparent du corps est pour cet observateur, pendant la deuxième seconde, ce qu'il était pour nous pendant la première, la mécanique classique concluait que sa vitesse doublait pendant cette deuxième seconde. C'est qu'elle ne savait pas ce qu'Einstein nous a enseigné: que le temps et l'espace dont se sert cet observateur sont différents des nôtres.

Qu'est-ce qu'une vitesse? C'est l'espace parcouru pendant une seconde. Mais l'espace que mesure ainsi notre observateur en mouvement, et qu'il croit avoir une certaine longueur, est, en réalité, pour nous immobiles, plus petit qu'il ne croit, parce que les mètres dont il se sert, sont—Einstein nous l'a montré,—raccourcis par la vitesse, sans qu'il puisse s'en apercevoir.

Et alors les vitesses ne s'ajoutent plus exactement [87] et au delà de toute limite pour un observateur donné, comme le voulait la mécanique classique.

Sous l'action d'une même force, disait cette mécanique, un corps subira toujours la même accélération, quelle que soit la vitesse déjà acquise. Sous l'action d'une même force, dit la mécanique nouvelle, le mouvement d'un corps s'accélérera d'autant moins qu'il sera plus rapide.

Voici par exemple un mobile. Dans le langage des physiciens, ce mot n'a pas du tout le même sens que dans celui des moralistes, puisque, pour les premiers, il signifie un corps en mouvement, et pour ceux-ci au contraire ce qui met un corps en mouvement! Sans m'appesantir sur toutes les réflexions que suggère cette antinomie verbale, qui n'est qu'un exemple de tout ce qui sépare la morale de la physique, je tiens à préciser que je prends ici ce mot dans le sens des physiciens.

Soit donc un mobile animé par rapport à moi d'une vitesse de 200 000 kilomètres par seconde. Sur ce premier mobile plaçons un observateur. Celui-ci projettera dans le même sens, et dans les mêmes conditions que nous avons fait, un deuxième mobile qui aura donc par rapport à lui une vitesse de 200 000 kilomètres. Mais, dit le relativiste, la vitesse résultante de ce deuxième mobile par rapport à nous ne sera pas, comme le voudrait l'addition classique des vitesses, 200 000 + 200 000 = 400 000 kilomètres par seconde. Elle sera seulement 277 000 kilomètres par seconde. [88] Ce que le deuxième observateur en mouvement croyait être 200 000 kilomètres (parce que ses règles étaient raccourcies par sa vitesse) ne valait donc en réalité que 77 000 de nos kilomètres. Comment peut-on calculer cela? Mais très simplement en appliquant la formule de Lorentz que j'ai indiquée dans le chapitre ii et qui donne la valeur de la contraction due à la vitesse. On trouve alors très aisément ceci: si on a deux vitesses v₁ et v₂, et si on appelle w leur résultante, la mécanique classique affirmait que

La mécanique d'Einstein enseigne que cela n'est pas exact et que l'on a en réalité (C étant la vitesse de la lumière)

.

Je m'excuse d'introduire de nouveau (ce sera la dernière fois!) une formule algébrique dans cet exposé. Mais elle m'épargne un très grand nombre de périphrases et même de phrases, et elle est d'une telle simplicité que tous les lecteurs,—et ils sont assurément nombreux,—ayant la moindre teinture de mathématiques élémentaires, en saisiront immédiatement la vaste signification et les conséquences.

Cette formule exprime d'abord que, si grande qu'elle soit, la résultante de deux vitesses ne peut dépasser la vitesse de la lumière. Elle exprime aussi [89] que si l'une des vitesses composantes est celle de la lumière, la vitesse résultante a, elle aussi, la même valeur. Elle exprime enfin qu'aux faibles vitesses auxquelles nous avons affaire dans la pratique (c'est-à-dire lorsque les vitesses composantes sont beaucoup plus petites que celle de la lumière) la résultante est, à très peu près, égale à la somme des deux composantes, comme le voulait la mécanique classique.

Celle-ci a été, ne l'oublions jamais, édifiée sur l'expérience. On comprend, dans ces conditions, que Galilée et ses successeurs, n'ayant eu affaire qu'à des mobiles relativement lents, soient arrivés à un principe apparemment vrai pour eux, mais qui n'est qu'une première approximation.

Par exemple, la résultante de deux vitesses, égales chacune à 100 kilomètres par seconde (ce qui dépasse infiniment les vitesses réalisables jadis par Galilée et Newton), est égale non pas à 200 kilomètres, mais à 199 km. 999 978. La différence est à peine de 22 millimètres sur 200 kilomètres! On conçoit que les expériences anciennes n'aient pu manifester des différences bien en deçà de celle-ci.

Parmi les vérifications de la nouvelle loi de composition des vitesses, on peut en citer une qui est frappante et qui ressort d'une expérience déjà ancienne de notre grand Fizeau.

[90] Supposons un tuyau plein d'un liquide, d'eau par exemple, et que parcourt dans sa longueur un rayon lumineux. On connaît la vitesse de la lumière dans l'eau (qui est bien inférieure à sa valeur dans l'air ou dans le vide). Supposons maintenant que l'eau ne soit plus immobile dans le tuyau, mais coule, circule dans celui-ci avec une certaine vitesse. Quelle sera, à la sortie du tuyau, la vitesse du rayon lumineux ayant traversé ce liquide en mouvement? C'est ce que Fizeau s'est demandé, en variant les conditions de l'expérience.

La vitesse de la lumière dans l'eau est d'environ 220 000 kilomètres par seconde. Il s'agit ici d'une propagation si rapide qu'il y a une grande différence entre la loi d'addition classique et celle de la mécanique einsteinienne. Or les résultats de l'expérience de Fizeau concordent rigoureusement avec la formule d'Einstein et sont en désaccord avec celle de la mécanique ancienne. De nombreux observateurs, et récemment le physicien hollandais Zeeman, ont repris avec une extrême précision l'expérience de Fizeau, et les résultats ont été identiques.

Lorsqu'au siècle passé Fizeau fit cette expérience, on avait certes essayé d'en interpréter les résultats numériques à la lumière des anciennes théories. Mais cela avait conduit à des hypothèses tout à fait invraisemblables. C'est ainsi que Fresnel, pour expliquer les résultats de Fizeau, avait été obligé d'admettre que l'éther est partiellement entraîné par l'eau dans son mouvement, mais que cet entraînement partiel varie [91] avec la longueur des ondes lumineuses propagées, et n'est pas la même pour les rayons bleus et pour les rayons rouges! Conséquence choquante et bien difficile à admettre.

La nouvelle loi de composition des vitesses donnée par Einstein rend compte, au contraire, immédiatement, et avec une extrême exactitude, des résultats de Fizeau. Ceux-ci sont en contradiction avec la loi classique.

Les faits, arbitres et critères souverains, montrent ici que la mécanique nouvelle correspond à la réalité, l'ancienne non, du moins sous sa forme traditionnelle.

Et voilà qui déjà nous fait toucher du doigt la beauté, la vérité profonde (la vérité scientifique étant ce qui est vérifiable) de la doctrine einsteinienne. Voilà qui nous démontre dès maintenant en quoi, magnifiquement, une théorie scientifique, une théorie physique se distingue d'un système philosophique arbitraire et plus ou moins cohérent.

L'expérience, juge suprême, décide en faveur de la mécanique einsteinienne, contre la mécanique classique. Nous en verrons d'autres exemples. Nous n'en trouverons aucun qui prononce en sens contraire.

Mais voici bien autre chose. La nouvelle loi de composition des vitesses, et l'existence d'une vitesse-limite égale à celle de la lumière, peuvent s'exprimer dans un [92] langage différent de celui que nous avons employé jusqu'ici. Nous n'avons encore parlé que de vitesses, de mouvements. Voyons comment les choses se présentent lorsque nous examinons en même temps les qualités particulières des objets qui se meuvent, des corps, de la matière.

Chacun sait que ce qui caractérise la matière, c'est ce qu'on appelle l'inertie. Si la matière est en repos, il faut une force pour la mettre en mouvement. Si elle est en mouvement, il faut une force pour l'arrêter. Il en faut une pour accélérer le mouvement. Il en faut une pour le dévier. Cette résistance que la matière oppose aux forces qui tendent à modifier son état de repos ou de mouvement, c'est ce qu'on appelle l'inertie. Les divers corps peuvent opposer à ces forces une résistance plus ou moins grande. Si une force est appliquée à un objet, elle lui imprimera une certaine accélération. Mais la même force appliquée à un autre objet lui imprimera en général une accélération différente. Un cheval de course déployant son effort maximum détalera plus vite s'il porte un minuscule jockey, que s'il porte un cavalier de cent kilos. Un cheval de trait démarrera plus rapidement si le chariot qu'il traîne est vide que s'il est chargé de marchandises. Vous pourrez mettre une charrette en mouvement avec le même effort qui n'ébranlerait pas un lourd camion.

Lorsqu'une locomotive traînant quelques wagons démarre brusquement, la vitesse imprimée au train au bout de la première seconde est (à une constante près) [93] ce qu'on appelle son accélération. Si cette locomotive démarre dans les mêmes conditions avec un train beaucoup plus long, on remarque que l'accélération est plus petite. De là provient la notion, introduite dans la science par Newton, de la masse des corps qui en mesure l'inertie.

Si, dans notre exemple, la locomotive produit la seconde fois une accélération deux fois plus petite, cela s'exprime en disant que la masse du deuxième train est double de celle du premier. Si on trouve que l'accélération produite par la locomotive est la même pour trois wagons chargés de blé et pour un seul wagon chargé de lingots, on dira que les deux trains ont la même masse totale.

En un mot, les masses des corps sont des données conventionnelles définies par ce fait qu'elles sont proportionnelles aux accélérations causées par une même force. Autrement dit, la masse d'un corps est le quotient de la force qui agit sur lui par l'accélération qu'il lui imprime. Poincaré disait pittoresquement: Les masses sont des coefficients qu'il est commode d'introduire dans les calculs.

S'il est une propriété des objets qui tombe sous le sens, sous les sens, dont chaque homme ait en quelque sorte l'instinct, l'intuition, c'est bien celle de la masse des corps. Eh bien! une analyse un peu aiguë nous montre donc notre impuissance à définir cette chose autrement que par des conventions déguisées. La définition poincariste semble paradoxale dans son aveu [94] d'impuissance. Elle est juste pourtant. La masse n'est qu'un «coefficient», qu'une création conventionnelle de notre infirmité!

Pourtant quelque chose nous restait où nous pensions pouvoir accrocher, sinon notre besoin de certitude,—il y a longtemps que les savants dignes de ce nom ont renoncé à la certitude!—du moins notre besoin de netteté dans la déduction, dans le classement des phénomènes. On croyait constante la masse, on croyait constant le coefficient si commode et si bien défini.

Ici encore, il faut déchanter, hélas!—ou plutôt tant mieux, puisque rien n'égale, après tout, le savoureux plaisir de la nouveauté.

L'ancienne mécanique nous enseignait que la masse est constante pour un même corps, indépendante par conséquent de la vitesse que ce corps a déjà acquise. D'où il suivait, comme nous l'expliquions plus haut, que, si une force continue à agir, la vitesse acquise au bout d'une seconde sera doublée au bout de deux secondes, triplée au bout de trois et ainsi de suite jusqu'au delà de toute limite.

Mais nous venons de voir que la vitesse augmente moins pendant la deuxième seconde que pendant la première et ainsi de suite, toujours de moins en moins jusqu'à ce que, la vitesse de la lumière étant atteinte, celle du mobile ne puisse plus augmenter, quelle que soit la force agissante.

Qu'est-ce à dire? Si la vitesse du corps s'accroît moins pendant la deuxième seconde, c'est qu'il oppose [95] à la force accélératrice une résistance plus grande. Tout se passe comme si son inertie, comme si sa masse avait changé! Cela revient à dire: la masse des corps n'est pas constante, elle dépend de leur vitesse, elle croît quand cette vitesse croît.

Pour les petites vitesses cette influence est insensible. Parce qu'ils n'avaient pu observer que celles-là, les fondateurs de la mécanique classique,—science expérimentale,—ont remarqué que les masses étaient sensiblement constantes, et en ont cru pouvoir conclure qu'elles l'étaient absolument. Aux grandes vitesses cela n'est plus vrai.

Pareillement, aux petites vitesses, dans la mécanique nouvelle comme dans l'ancienne, les corps opposent sensiblement la même résistance d'inertie aux forces qui tendent à accélérer leur mouvement et à celles qui tendent à le dévier, à courber leur trajectoire. Aux grandes vitesses cela n'est plus vrai.

La masse croît donc rapidement avec la vitesse, jusqu'à devenir infinie quand cette vitesse égale celle de la lumière. Un corps quelconque ne pourra jamais atteindre ni dépasser la vitesse de la lumière, puisque, pour dépasser cette limite, il faudrait surmonter une résistance infinie.

Voici, pour fixer les idées, quelques chiffres qui laissent voir dans quelles proportions les masses varient avec la vitesse. Le calcul est facile, grâce à la formule que nous avons indiquée et qui donne les valeurs de la contraction de Fitzgerald-Lorentz.

[96] Une masse de 1 000 grammes pèsera 2 centigrammes de plus à la vitesse de 1 000 kilomètres par seconde; elle pèsera 1 060 grammes à la vitesse de 100 000 kilomètres par seconde; 1 341 grammes à la vitesse de 200 000 kilomètres par seconde; 2 000 grammes (elle aura doublé) à la vitesse de 259 806 kilomètres par seconde; 3 905 grammes à la vitesse de 290 000 kilomètres par seconde.

Voilà ce qu'indique la théorie nouvelle. Comment la vérifier? Cela eût été impossible il y a encore cinquante ans, alors qu'on ne connaissait que nos pauvres petites vitesses de véhicules et de projectiles terrestres, qui alors ne dépassaient jamais, même pour les obus, 1 kilomètre par seconde. Les planètes elles-mêmes n'ont que des vitesses bien trop faibles pour cette vérification et Mercure, par exemple, qui est la plus rapide de toutes, ne fait que du 100 kilomètres à la seconde, ce qui est encore insuffisant.

Si nous n'avions disposé que de vitesses comme celles-là, il n'y aurait pas eu moyen de vérifier qui avait raison, de la mécanique classique affirmant la masse constante, ou de la mécanique nouvelle l'affirmant variable.

Ce sont les rayons cathodiques et les rayons Bêta du radium qui nous ont fourni des vitesses suffisantes pour une vérification.

[97] Ces rayons sont constitués par un bombardement ininterrompu de petits projectiles très rapides, d'une masse inférieure à la deux-millième partie de celle de l'atome d'hydrogène, chargés d'ailleurs d'électricité négative et qu'on appelle des électrons.

Les tubes cathodiques et le radium effectuent un bombardement continuel de ces petits projectiles chargés non pas de mélinite, mais d'électricité, bien moins gros que les obus des artilleries européennes, mais en revanche animés de vitesses initiales infiniment plus grandes et auprès desquelles celle de Bertha même fait très piètre figure.

Comment maintenant a-t-on pu mesurer la vitesse de ces projectiles?

On sait que les corps électrisés agissent les uns sur les autres: ils s'attirent ou se repoussent. Nos électrons sont chargés d'électricité. Si donc on les place dans un champ électrique, entre deux plateaux réunis aux deux bornes d'une machine électrique ou d'une bobine d'induction, ils vont être soumis à une force qui les déviera de leur route. Les rayons cathodiques seront donc déviés par un champ électrique. Cette déviation dépendra de la vitesse des projectiles et elle dépendra aussi de leur masse, c'est-à-dire de la résistance d'inertie qu'elle oppose aux causes qui tendent à la dévier.

Ce n'est pas tout. Les charges électriques portées par ces projectiles sont en mouvement, et même en mouvement rapide. De l'électricité en mouvement, [98] c'est un courant électrique; or nous savons que les courants sont déviés par les aimants, par les champs magnétiques. Les rayons cathodiques seront donc déviés par l'aimant. Cette déviation, comme la première, dépendra de la vitesse et de la masse du projectile. Seulement, elle n'en dépendra pas de la même manière. Toutes choses égales d'ailleurs, la déviation magnétique sera plus grande que la déviation électrique si la vitesse est grande. En effet, la déviation magnétique est due à l'action de l'aimant sur le courant; elle sera d'autant plus grande que le courant sera plus intense; et le courant sera d'autant plus intense que la vitesse sera plus grande, puisque c'est le mouvement du projectile qui produit le courant. Au contraire, la trajectoire de nos petits projectiles, sous l'influence de l'attraction électrique, sera d'autant moins déviée que le projectile sera plus rapide.

On conçoit donc qu'en soumettant un rayon cathodique à l'action d'un champ électrique, puis à celle d'un champ magnétique, on puisse, en comparant les deux déviations, mesurer à la fois la vitesse du projectile et sa masse (rapportée à la charge électrique connue de l'électron).

On trouve ainsi des vitesses énormes allant de plusieurs dizaines de kilomètres jusqu'à 150 000 kilomètres par seconde et davantage. Quant aux rayons Bêta du radium, ils sont encore plus rapides et atteignent jusqu'à des vitesses très voisines de celle de la lumière et supérieures à 290 000 kilomètres par seconde. [99] Voilà bien les vitesses qu'il nous faut pour voir si, oui ou non, la masse augmente avec elles.

Cela posé, et pour comprendre parfaitement la marche des expériences, il nous reste à dire quelques mots de ce curieux phénomène d'inertie électrique qu'on appelle la self-induction. Quand on veut établir un courant électrique, on éprouve une certaine résistance initiale qui cesse dès que le courant est établi; si ensuite on veut rompre le courant, il tend à se maintenir et on a autant de mal à l'arrêter qu'à arrêter une voiture une fois lancée. L'expérience journalière peut le montrer. Quelquefois les trolleys d'un tramway quittent un instant le fil qui amène le courant; à ce moment, on voit jaillir des étincelles. Pourquoi? Il passait un courant qui allait du fil au trolley; si le trolley s'éloigne un instant du fil, laissant un intervalle d'air qui est un obstacle au passage de l'électricité, le courant ne s'arrête pas pour cela, parce qu'il est lancé pour ainsi dire; il franchit l'obstacle sous forme d'étincelle. Ce phénomène est ce qu'on appelle la self-induction.

La self-induction ou simplement la self, comme disent les ouvriers électriciens, est une véritable inertie. Le milieu ambiant oppose une résistance à la force qui tend à établir un courant électrique et à celle qui tend à faire cesser un courant préalablement établi, de même [100] que la matière résiste à la force qui tend à la faire passer du repos au mouvement, ou au contraire du mouvement au repos. Il y a donc, à côté de l'inertie mécanique, une véritable inertie électrique.

Mais nos projectiles cathodiques, nos électrons sont chargés. Quand ils se mettent en mouvement, ils font naître un courant électrique; quand ils s'arrêtent, le courant cesse. A côté de l'inertie mécanique, ils doivent donc posséder également l'inertie électrique. Ils ont pour ainsi dire deux inerties, c'est-à-dire deux masses inertes, une masse réelle et mécanique, et une masse apparente due aux phénomènes de self-induction électro-magnétique. En étudiant les deux déviations, électrique et magnétique, des rayons Bêta du radium ou des rayons cathodiques, on peut déterminer quelle est, dans la masse totale de l'électron, la part de ces deux masses. En effet, la masse électro-magnétique due aux causes que nous venons d'expliquer varie avec la vitesse, suivant certaines lois que la théorie de l'électricité nous fait connaître. En observant la relation entre la masse totale et la vitesse, on peut donc voir quelle est la part de la masse véritable et invariable, et celle de la masse apparente d'origine électro-magnétique.

L'expérience a été réalisée et répétée par des physiciens très habiles. Le résultat est bien fait pour surprendre: la masse réelle est nulle, toute la masse de la particule est d'origine électro-magnétique. Voilà qui est de nature à modifier complètement nos idées sur [101] l'essence de ce qu'on nomme matière. Mais ceci, est une autre histoire....

On s'est demandé alors,—et c'est là que nous voulions en venir après ces quelques détours qui auront débroussaillé le chemin,—si la relation entre la masse et la vitesse des projectiles cathodiques, était la même que celle où nous avait conduits le principe de relativité.

Le résultat des expériences est absolument net et concordant et certaines d'entre elles ont porté sur des rayons Bêta correspondant à une valeur de la masse décuple de la masse initiale. Ce résultat est celui-ci: les masses varient avec la vitesse et exactement suivant les lois numériques de la dynamique d'Einstein.

Nouvelle et précieuse confirmation expérimentale, et qui tend à établir, elle aussi, que la mécanique classique n'était qu'une grossière approximation, valable tout au plus pour les médiocres vitesses auxquelles nous avons affaire dans le cours ridiculement borné de la vie quotidienne.

Ainsi la masse des corps, cette propriété newtonienne qu'on croyait le symbole même de la constance et l'équivalent de ce qu'est, dans l'ordre des choses morales, la fidélité aux traités, n'est plus qu'un petit coefficient variable, ondoyant et relatif selon le point de vue. En vertu de la réciprocité que nous avons déjà précisée, lorsqu'il s'est agi de la contraction due à la vitesse, la masse d'un objet augmente pareillement non seulement s'il se déplace, mais si celui qui l'observe se déplace, [102] et sans d'ailleurs qu'un autre observateur lié à l'objet puisse jamais constater la différence.

Ainsi, une règle qui se meut à une vitesse d'environ 260 000 kilomètres par seconde aura non seulement sa longueur diminuée de moitié, mais en même temps sa masse doublée. Sa densité, qui est le rapport de sa masse à son volume, sera donc quadruplée.

Les notions physiques qu'on croyait les mieux établies, les plus constantes, les plus inébranlables deviennent, déracinées par l'ouragan de la mécanique nouvelle, des choses flottantes, molles, plastiques et que modèle la vitesse.

D'autres vérifications de la formule nouvelle, et tout à fait indépendantes de celle que nous venons d'exposer, ont été fournies récemment par les physiciens.

L'une des plus étonnantes est apportée par la spectroscopie.

On sait, que lorsqu'on fait passer un rayon de lumière solaire, provenant d'une fente fine, à travers l'arête d'un prisme de verre, ce rayon s'étale à la sortie du prisme, comme un magnifique éventail dont les lames successives sont constituées par les couleurs de l'arc-en-ciel. Dans cet éventail coloré une observation attentive fait reconnaître de fines discontinuités, des lacunes [103] étroites où il n'y a pas de lumière; on dirait des coupures faites par des ciseaux dans l'éventail polychrome, et qui sont les raies sombres du spectre solaire. Chacune de ces raies correspond à un élément chimique déterminé et sert à l'identifier tant au laboratoire que dans le Soleil ou les étoiles.

On a depuis longtemps expliqué que ces raies proviennent des électrons tournant très rapidement autour du centre de l'atome. Leurs changements soudains de vitesse produisent dans le milieu ambiant une onde (pareille à celle causée dans l'eau par la chute d'un caillou) et qui est une des ondes lumineuses caractéristiques de l'atome. Elle se manifeste par une des raies du spectre. Le physicien danois Bohr a récemment développé cette théorie dans tous ses détails, qui importent peu ici, et montré qu'elle rend compte avec exactitude des diverses raies spectrales correspondant aux éléments chimiques. Ceux-ci, je le rappelle, diffèrent entre eux par le nombre et la disposition des électrons gravitant dans leurs atomes.

Or M. Sommerfeld a fait le raisonnement suivant: les électrons qui gravitent près du centre d'un atome doivent avoir une vitesse beaucoup plus grande que ceux qui gravitent vers l'extérieur, de même que les planètes inférieures, Mercure et Vénus, ont autour du Soleil des vitesses bien plus grandes que les planètes supérieures, Jupiter, Saturne. Il s'ensuit,—si les idées de Lorentz et d'Einstein sont exactes,—que la masse des électrons internes des atomes doit être plus grande [104] que celle des électrons externes, sensiblement plus grandes, car ces électrons tournent à des vitesses énormes. Le calcul montre alors que, dans ces conditions, chaque raie du spectre d'un élément chimique doit être en réalité composée d'un ensemble de plusieurs petites raies fines et juxtaposées. C'est précisément ce qui a été postérieurement (1916) constaté par Paschen. Il a trouvé que la structure des raies fines est très rigoureusement celle qu'annonçait Sommerfeld. Étonnante confirmation de l'hypothèse faite: exactitude de la nouvelle mécanique!

Mais ce n'est pas tout. On sait que les rayons X sont des vibrations analogues à la lumière, de même origine, mais de longueur d'onde beaucoup plus courte, c'est-à-dire d'une plus grande fréquence. Donc, tandis que la lumière provient des électrons extérieurs de ce petit système solaire en miniature qu'est l'atome, les rayons X proviennent des électrons les plus rapides, c'est-à-dire les plus proches du centre. Il s'ensuit que la structure particulière des raies fines, due à la variation de la masse électronique avec la vitesse, doit être bien plus marquée encore pour les raies des rayons X que pour les raies spectrales de la lumière. C'est effectivement ce que l'expérience a constaté. Les chiffres caractérisant les faits observés correspondent exactement aux calculs de la mécanique nouvelle, à la variation prévue de la masse avec la vitesse.

Il est donc établi que les phénomènes qui ont lieu dans le microcosme de chaque atome obéissent aux lois [105] de la mécanique nouvelle, et non de l'ancienne, et qu'en particulier les masses en mouvement y varient comme le veut celle-là.

L'expérience, «source unique de toute vérité», a prononcé.

Nous voilà bien loin des idées naguère courantes. Lavoisier nous a enseigné que la matière ne peut se créer ni se détruire, qu'elle se conserve. Ce qu'il a voulu dire par là, c'est que la masse est invariable, et il l'a vérifié avec la balance. Et voici maintenant que les corps n'ont peut-être plus de masse,—si elle est entièrement d'origine électro-magnétique,—et voici en tout cas que cette masse n'est plus invariable. Cela ne veut pas dire que la loi de Lavoisier n'ait plus de sens. Il subsiste quelque chose qui se confond avec la masse aux petites vitesses. Mais enfin notre conception de la matière est violemment bouleversée. Ce que nous appelions matière, c'était avant tout la masse, qui était en elle ce qui nous semblait de plus tangible à la fois et de plus durable. Et maintenant cette masse n'existe pas plus que le temps et l'espace où nous croyions pouvoir la situer! Ces réalités n'étaient que des fantômes....

Qu'on me pardonne ce que cet exposé a d'un peu ardu. Mais la nouvelle mécanique nous ouvre des horizons si étrangement nouveaux qu'elle vaut mieux qu'un regard dédaigneux et rapide. Pour contempler un vaste paysage dans un monde inexploré, il ne faut pas hésiter, même au prix d'un essoufflement passager, à grimper parfois une côte un peu rude.

[106]

Il est enfin une autre notion fondamentale de la mécanique, la notion d'énergie qui, à la lumière de la théorie einsteinienne, nous apparaît sous un aspect inattendu et justifié dans une large mesure, lui aussi, par l'expérience.

Nous avons vu qu'un corps chargé d'électricité et en mouvement oppose une certaine résistance au déplacement, par suite de cette inertie électrique qu'on appelle la self-induction. Le calcul et l'expérience montrent que, si on diminue les dimensions du corps portant une certaine quantité d'électricité, sans changer celle-ci, cette inertie électrique augmente. En effet, dans les hypothèses faites et si l'inertie est d'origine exclusivement électro-magnétique, les électrons ne sont plus que des sortes de sillages électriques se mouvant dans ce milieu propagateur des ondes électriques et lumineuses qu'on appelle l'éther.

Les électrons ne sont plus rien par eux-mêmes; ils sont seulement, suivant l'expression de Poincaré, des sortes de «trous dans l'éther», autour desquels s'agite celui-ci, à la manière d'un lac faisant des remous qui résistent à l'avancement d'un esquif.

Mais alors, plus les trous dans l'éther seront petits, plus l'agitation de l'éther autour d'eux sera proportionnellement importante. Plus, par conséquent, l'inertie du «trou dans l'éther» qui constitue le corpuscule étudié [107] sera grande. Que va-t-il s'ensuivre? On sait, par les mesures faites, que la masse du petit soleil de chaque atome, du noyau positif,—autour duquel tournent les planètes électrons,—on sait, dis-je, que ce noyau positif a une masse beaucoup plus grande que celle d'un électron. Si cette masse, si l'inertie correspondante sont ici aussi d'origine électro-magnétique, il s'ensuit donc que le noyau positif des atomes est beaucoup plus petit que l'électron.

Si nous considérons l'atome de l'hydrogène, le plus léger et le plus simple des gaz, nous savons qu'il est formé par une seule planète, par un seul électron négatif tournant autour du petit soleil central, autour du noyau positif. Nous savons aussi que la masse de l'électron est 2 000 fois plus petite que celle de l'atome d'hydrogène. Il suit de tout cela, le calcul le montre, que le noyau positif doit avoir un rayon 2 000 fois plus petit que celui de l'électron. Or, les expériences des physiciens anglais ont établi que les grosses particules alpha des rayons du radium peuvent traverser plusieurs centaines de milliers d'atomes, sans être déviées sensiblement par le noyau positif. On en déduit que celui-ci est en effet bien plus petit que l'électron, conformément aux prévisions théoriques.

Tout cela conduit irrésistiblement à penser que l'inertie de toutes les parties constituantes des atomes, c'est-à-dire de toute la matière, est exclusivement d'origine électro-magnétique. Il n'y a plus de matière, il n'y a plus que de l'énergie électrique, qui, par les [108] réactions que le milieu ambiant exerce sur elle, nous fait croire fallacieusement à l'existence de ce quelque chose de substantiel et de massif que les générations ont accoutumé d'appeler matière.

Mais de tout cela il ressort aussi par des calculs et des raisonnements simples et élégants d'Einstein,—et dont je ne puis ici que laisser deviner la marche,—que la masse et l'énergie sont la même chose, ou du moins sont les deux faces d'une même médaille. Donc, plus de masse matérielle, rien que de l'énergie dans l'univers sensible. Étrange aboutissement, presque spiritualiste en un sens, de la physique moderne!

D'après tout cela, la plus grande partie de la «masse» des corps serait due à une énergie interne considérable et cachée. C'est cette énergie que nous voyons se dissiper peu à peu dans les corps radioactifs, seuls réservoirs d'énergie atomique ouverts jusqu'ici sur l'extérieur.

Si tout cela est vrai, si énergie et masse sont synonymes, si la masse n'est que de l'énergie, réciproquement l'énergie libre doit posséder des propriétés massives. Effectivement, la lumière par exemple a une masse. Des expériences précises ont en effet montré qu'un rayon de lumière, frappant un objet matériel, exerce sur lui une pression qui a été mesurée. La lumière a une masse, donc elle a un poids comme toutes les masses. Nous verrons d'ailleurs, à propos de la nouvelle forme donnée par Einstein au problème de la gravitation, une autre preuve directe,—et combien belle!—que la lumière est pesante.

[109] On peut calculer que la lumière reçue du Soleil sur la Terre en l'espace d'une année pèse un peu plus de 58 000 tonnes. C'est peu si l'on songe au poids formidable de charbon qu'il faudrait pour entretenir sur ce globule terraqué la température assez douce, en somme, qu'y maintient le Soleil,... au cas où celui-ci s'éteindrait brusquement.

La différence provient de ceci: quand nous nous chauffons avec un certain poids de charbon, nous n'utilisons qu'une faible partie de son énergie disponible, son énergie chimique. Toute son énergie intra-atomique nous reste inaccessible. C'est fâcheux, sans quoi il suffirait de quelques grammes de charbon pour chauffer, l'année durant, toutes les villes et toutes les usines de France. Que de problèmes en seraient simplifiés! Quand l'humanité sera sortie de l'ignorance et de la maladresse barbare où elle croupit, c'est-à-dire dans quelques centaines de siècles, nous verrons cela. Oui, nous verrons cela. Ce sera un beau spectacle en vérité, et dont on a le droit de se réjouir par avance.

En attendant, le Soleil, comme tous les astres, comme tous les corps incandescents, perd peu à peu de son poids à mesure qu'il rayonne. Mais avec une telle lenteur que nous n'avons pas à craindre de le voir, de si tôt, s'évanouir à nos yeux, pareil à ces êtres de choix qui meurent de s'être trop donnés.

[110]

Voici, pour en finir avec la mécanique d'Einstein, une bien suggestive application de ces idées sur l'identité de l'énergie et de la masse.

Il y a en chimie une loi élémentaire bien connue et qui s'appelle loi de Prout. Elle dit que les masses atomiques de tous les éléments doivent être des multiples entiers de celle de l'hydrogène. Celui-ci étant, de tous les corps connus, celui dont l'atome est le plus léger, la loi de Prout partait de l'hypothèse que tous les atomes sont construits d'après un élément fondamental qui est l'atome d'hydrogène. Cette unité supposée de la matière semble de plus en plus démontrée par les faits. D'une part, il est prouvé que les électrons provenant d'éléments chimiques différents sont identiques. D'autre part, dans les transformations des corps radioactifs nous voyons des atomes lourds émettre successivement plusieurs atomes du gaz hélium en se simplifiant. Enfin, le grand physicien britannique Rutherford a montré en 1919 qu'en bombardant, dans certaines conditions, au moyen des rayons du radium, les atomes du gaz azote, on peut en arracher des atomes d'hydrogène. Cette expérience, d'une importance qui n'a pas été assez aperçue et qui constitue en somme le premier exemple d'une transmutation réellement accomplie par l'homme, tend, elle aussi, à prouver la validité de l'hypothèse de Prout.

[111] Pourtant, lorsqu'on mesure exactement et qu'on compare les masses atomiques des divers éléments chimiques, on constate qu'elles ne suivent pas exactement la loi de Prout. Par exemple, la masse atomique de l'hydrogène étant 1, celle du chlore est 35,46, ce qui n'est pas un multiple entier de 1.

Or on peut calculer que si la formation des atomes complexes à partir de l'hydrogène s'accompagne,—comme il est probable,—de variation d'énergie interne, par suite d'une certaine quantité d'énergie rayonnée dans la combinaison, il s'ensuivra nécessairement (puisque l'énergie perdue est pesante) des variations de la masse du corps résultant qui rendent très bien compte des écarts constatés à la loi de Prout.

Dans notre promenade un peu hâtive, et en zig-zag, à travers la broussaille des faits nouveaux qui étayent et vérifient la mécanique ébauchée par Lorentz, achevée par Einstein, notre démarche a été assez heurtée. C'est que, faute de la terminologie et des formules techniques dont l'appareil, ici, serait par trop rébarbatif, on doit se contenter de quelques raids hardiment et rapidement poussés dans le secteur à reconnaître. Ils auront suffi, peut-être, pour comprendre quel bouleversement total des bases mêmes de la science, quelle explosion dans ses fondements séculaires a produite la fulgurante synthèse einsteinienne.

[112] Vraiment des lumières nouvelles rayonnent maintenant sur ceux qui, lentement, s'efforcent à la rude escalade du savoir, et, ayant sagement renoncé à chercher les «pourquoi», veulent du moins scruter quelques «comment».

Peu avant sa mort et prévoyant avec son intuition géniale l'avènement de la nouvelle mécanique, Poincaré conseillait aux professeurs de ne pas l'enseigner aux enfants avant qu'ils fussent pénétrés jusqu'aux moelles de la mécanique classique.

«C'est, ajoutait-il, avec la mécanique ordinaire qu'ils doivent vivre; c'est la seule qu'ils auront jamais à appliquer; quels que soient les progrès de l'automobile, nos voitures n'atteindront jamais les vitesses où elle n'est plus vraie. L'autre n'est qu'un luxe et l'on ne doit penser au luxe que quand il ne risque plus de nuire au nécessaire.»

Pour un peu, j'en appellerais de ce texte de Poincaré à Poincaré lui-même. Car pour lui, ce luxe, la vérité, était la seule chose nécessaire. Ce jour-là, assurément il songeait aux enfants. Mais les hommes cessent-ils jamais d'être des enfants? A cela le maître trop tôt disparu eût répondu peut-être, de sa voix grave adoucie d'un sourire: «Oui; du moins il est plus commode de le supposer.»

Les mêmes lois, nous le savons maintenant, régissent la mécanique et l'optique; s'il avait paru en être autrement c'est qu'aux vitesses voisines de celle de la lumière les longueurs et les masses des objets subissent, pour l'observateur, une variation qui [114] est insensible aux vitesses usuelles. C'est par sa puissance de synthèse que la mécanique einsteinienne est splendide. Grâce à elle nous apercevons dans le surprenant univers où passent, éphémères, nos pensées et nos angoisses, plus d'unité qu'auparavant, donc plus d'harmonie, plus de beauté.

Pourtant la théorie de la relativité laissait jusqu'ici de côté un phénomène fondamental, essentiel, répandu partout et toujours dans le cosmos: la gravitation, propriété mystérieuse des corps qui gouverne les atomes infimes aussi bien que les étoiles géantes et dirige leurs trajectoires suivant des courbes majestueuses.

L'attraction universelle que, sur la Terre, nous appelons pesanteur, était parmi les phénomènes une sorte d'île escarpée et sans rapport avec le reste de la philosophie naturelle.

La mécanique d'Einstein, telle que nous l'avons exposée jusqu'ici, passait à côté de cette île sans l'aborder. C'est pourquoi, sous cette forme, on l'appelait théorie de la relativité restreinte. Pour en faire un instrument de synthèse achevé, il restait à y faire entrer le phénomène de la gravitation. C'est par cela qu'Einstein a couronné son œuvre et que son système a pris la forme admirable désignée maintenant sous le nom de théorie de la relativité généralisée.

Einstein a tiré la gravitation universelle de son «splendide isolement», et l'a attachée, docile et vaincue, au char triomphal de sa mécanique. Bien plus, il a donné [115] de la loi célèbre de Newton une forme plus exacte et que l'expérience, juge sans appel, a reconnue la seule correcte.

Comment il y est parvenu, par quelle chaîne subtile et forte de raisonnements et de calculs fondés sur les faits, c'est ce que je vais m'efforcer maintenant d'exposer, en tâchant, une fois encore, d'éviter avec soin au passage les réseaux de fils barbelés de la terminologie mathématique.

Pourquoi Newton a-t-il cru—et toute la science classique après lui—que la gravitation, la chute des corps, ne rentre pas dans la mécanique dont il a formulé les lois? Pourquoi en un mot a-t-il considéré la gravitation comme une force, ou—pour employer un terme plus vague mais plus général—comme une action qui fait que les corps pesants ne se déplacent pas librement dans l'espace vide?

C'est à cause du principe d'inertie. Ce principe, base de toute la mécanique newtonienne, peut s'exprimer ainsi: un corps sur lequel n'agit aucune force conserve une vitesse et une direction invariables.

Pourquoi adjoint-on aux machines à vapeur ces roues massives qu'on appelle des «volants» et qui tournent à vide? Parce que le principe d'inertie est sûrement à peu près vrai. Lorsque la machine subit un à-coup, un arrêt brusque et bref, une accélération imprévue, le volant est là pour remettre les choses en état. Entraîné par sa vitesse acquise et entraînant à son tour la machine il tend à conserver cette vitesse et empêche et corrige aussi bien les ralentissements accidentels [116] que les accélérations. Ce principe est donc fondé sur l'expérience, et plus précisément sur celles de Galilée qui l'a vérifié en faisant rouler des billes sur des plans diversement inclinés.

Par exemple on constate qu'une bille lancée sur un plan horizontal parfaitement poli conserve une même direction et une vitesse qui resterait uniforme, si la résistance de l'air et le frottement sur le plan n'intervenaient pour la réduire peu à peu jusqu'à zéro. On observe en effet qu'en réduisant ces résistances de frottement la bille tend à conserver de plus en plus longtemps sa vitesse.

C'est sur une foule d'expériences analogues qu'est basé le principe d'inertie de Newton. Ce principe n'a donc nullement le caractère d'une vérité mathématique d'évidence. Cela est si vrai que les anciens, contrairement à notre mécanique classique, croyaient que le mouvement s'arrête dès que cesse la cause qui lui a donné naissance. Certains philosophes grecs avaient encore une autre manière de voir; ils pensaient que tout corps, si rien ne vient à le contrarier, prendra un mouvement circulaire, parce que c'est le plus noble de tous les mouvements.

Nous verrons plus loin comment le principe d'inertie de la mécanique généralisée d'Einstein s'apparente étrangement à cette dernière conception et en même temps à la curieuse déclinaison, au clinamen que le grand et profond Lucrèce attribuait à la trajectoire libre de ses atomes. Mais n'anticipons pas....

[117]

Cette affirmation qu'un objet abandonné librement à lui-même et soustrait à l'action de toute force garde sa vitesse et sa direction, ce principe d'inertie ne peut prétendre à être autre chose qu'une vérité d'expérience.

Or les observations qui servent de base à ce principe, celles de Galilée en particulier, et toutes celles que les physiciens pourraient imaginer, ne sauraient être parfaitement démonstratives, parce qu'il est impossible, dans la pratique, de soustraire complètement un mobile à l'action de toute force extérieure, résistance de l'air, frottement ou autre.

Je sais bien que Newton a fondé ce principe non pas seulement sur les observations terrestres, mais sur celles des astres. Il a remarqué que, abstraction faite de l'action attirante des autres corps célestes, et pour autant qu'il est possible d'en juger, les planètes semblent conserver leur direction et leur vitesse par rapport à la voûte étoilée. Mais les relativistes pensent que les mots soulignés dans la phrase précédente, et qui correspondent à la pensée de Newton, constituent une pétition de principe. Son raisonnement présuppose que les planètes ne circulent pas librement, qu'elles sont contraintes dans leur mouvement par une force que Newton a appelée attraction universelle.

Nous verrons comment Einstein a été amené à penser que celle-ci n'est peut-être pas une force, et alors [118] la conclusion du raisonnement est tout autre. Quoi qu'il en soit, le principe d'inertie classique est une vérité fondée sur des expériences (d'ailleurs toujours imparfaites), et qui comme telle doit rester sous le contrôle perpétuel des faits. Tout ce qu'on en peut affirmer c'est qu'il correspond pratiquement, c'est-à-dire à peu près, à ce qu'on constate.

Newton le considérait non pas de la sorte, non pas comme une approximation plus ou moins exacte mais comme une vérité rigoureuse.

C'est pourquoi, observant que les planètes se meuvent non en ligne droite, mais suivant des courbes, il en déduisait (ce qui est la pétition de principe incriminée) qu'elles étaient soumises à une force centrale, la gravitation. C'est pourquoi les corps pesants, les corps gravitants, ne lui semblaient pas justiciables des lois mécaniques qu'il avait d'abord établies pour les corps librement abandonnés à eux-mêmes. C'est pourquoi en un mot, la loi de gravitation de Newton, et les lois de la dynamique de Newton sont des choses distinctes et séparées.

Ce grand génie, ce cerveau sans égal était pourtant un cerveau humain. Notre immortel Descartes, après avoir décidé de ne rien affirmer que ce qu'il percevait clairement et distinctement, a cependant lancé des affirmations singulières et des hypothèses fort occultes sur la glande pinéale et les esprits animaux. Pareillement Newton après avoir posé en principe Hypotheses non fingo a placé à la base de sa mécanique les hypothèses [119] du temps absolu et de l'espace absolu. A la base de sa géniale théorie de la gravitation il a placé l'hypothèse—d'ailleurs plus admissible a priori—de l'existence d'une force gravitationnelle particulière.

Ce sont là des faiblesses inhérentes aux plus grands hommes. Elles doivent nous faire admirer davantage les côtés lumineux de leur œuvre. Tant est profond, même lorsqu'il dévie de la ligne droite, le sillon creusé par ces grands défricheurs de l'inconnu, que deux siècles et demi ont passé avant qu'on songe même à rechercher si la discrimination faite par Newton entre les phénomènes purement mécaniques et les phénomènes gravitationnels est réellement fondée.

Le grand honneur d'Einstein est de l'avoir victorieusement tenté; son honneur, après avoir fait table rase de maintes acquisitions qu'on croyait définitives, est d'avoir fondu la gravitation et la mécanique dans une synthèse superbe, et de nous avoir mieux fait sentir l'Unité sublime du monde.

Au vrai, et avant même de pénétrer plus loin dans les allées profondes et merveilleuses de la relativité généralisée, il est évident a priori que la loi de l'attraction universelle de Newton ne peut plus être maintenant considérée comme satisfaisante.

[120] Elle affirme: Les corps s'attirent en raison directe de leurs masses et en raison inverse du carré de leurs distances. Qu'est-ce à dire? Nous avons vu que les masses des corps varient avec leurs vitesses. Lorsqu'on introduit par exemple la masse de la planète Terre dans les calculs où intervient la loi de Newton, de quoi s'agit-il donc? S'agit-il de la masse qu'aurait la Terre si elle ne tournait pas autour du Soleil? S'agit-il au contraire de la masse plus grande qu'elle possède par suite de sa translation? Mais cette translation n'a pas toujours la même rapidité puisque la Terre décrit une ellipse et non un cercle? Et alors quelle valeur de cette masse variable introduira-t-on dans le calcul? Celle qui correspond au périhélie ou à l'aphélie, à l'époque où la Terre se déplace le plus vite, ou à celle qui ralentit son mouvement orbital? D'ailleurs ne devra-t-on pas tenir compte aussi de la vitesse de translation du système solaire qui, selon les saisons, augmente ou diminue celle de la Terre.

D'autre part dans la loi de Newton, qu'introduirons-nous comme distance de la Terre au Soleil? Sera-ce la distance relative à un observateur placé sur la Terre ou sur le Soleil, ou au contraire immobile au centre de la Voie Lactée et ne participant pas au mouvement de notre système à travers celle-ci? Ici encore on aura des valeurs différentes suivant les cas, puisque les distances spatiales varient, nous l'avons vu avec Einstein, selon la vitesse relative de l'observateur.

La loi de Newton, en dépit de sa forme si simple, si [121] esthétique, est donc ambiguë et peu nette. Je sais bien que les différences dont nous venons de parler sont faibles; mais elles ne sont pas pour cela négligeables, le calcul le montre.

Sous sa forme classique, il est donc certain pour les einsteiniens et sans préjudice des considérations où nous allons entrer, que la loi de Newton est obscure et doit être modifiée et complétée.

Ces remarques préliminaires auront peut-être ceci d'utile, qu'elles nous achemineront vers l'état d'esprit un peu nécessaire aux iconoclastes... et dans la science les iconoclastes sont parfois les ouvriers du progrès. Les idoles auxquelles ces remarques nous habitueront à voir porter quelques coups injurieux sont la conception et la loi newtoniennes de la gravitation.

Laplace a écrit dans son exposition du système du monde: «Il est impossible de ne pas convenir que rien n'est mieux démontré dans la philosophie naturelle que le principe de la gravitation universelle en raison des masses et réciproque au carré des distances.»

Rien ne mesure aussi bien que cette phrase d'un savant illustre la grandeur du progrès accompli par Einstein lorsqu'il a, comme nous allons voir, perfectionné ce qu'on croyait le symbole même, l'exemple le plus achevé de la vérité scientifique: la loi célèbre de Newton.

[122]

La gravitation, la pesanteur a ceci de commun avec l'inertie des corps, qu'elle est un phénomène parfaitement général. Tous les objets matériels, tous les corps quel que soit leur état physique et chimique sont à la fois inertes (c'est-à-dire qu'ils résistent suivant leur masse aux forces tendant à les déplacer) et pesants, (c'est-à-dire qu'ils tombent lorsqu'ils sont librement abandonnés).

Mais il est une chose curieuse, que Newton avait déjà constatée sans en apercevoir la signification et qu'il considérait comme une simple et extraordinaire coïncidence: le nombre qui définit l'inertie d'un corps est le même qui définit son poids. Ce nombre c'est la masse.

Reprenons l'exemple qui m'a servi dans un chapitre précédent à propos de la mécanique d'Einstein. Si deux trains tirés par deux locomotives identiques démarrent dans les mêmes conditions et que la vitesse communiquée au premier train au bout d'une seconde soit double de celle du second, on en déduira que l'inertie, la masse inerte du second train (abstraction faite des frottements des rails) est deux fois plus grande que celle du premier. Or si nous mettons ensuite nos deux trains sur la bascule, nous constatons que le poids du second est, de même, deux fois plus grand que celui du premier.

Cette expérience qui, sous la forme que nous lui [123] donnons est grossière, a été faite avec une extrême précision par les physiciens au moyen de méthodes délicates qui importent peu ici. Le résultat a été semblable: la masse inerte et la masse pesante des corps sont exprimées rigoureusement par les mêmes nombres.

Newton n'avait vu là qu'une coïncidence. Einstein y a trouvé la clef du donjon hermétique et inviolé où la gravitation s'isolait du reste de la nature.

Voici comment:

Une chose est remarquable dans la pesanteur, dans la gravitation: quelle que soit la nature des objets, ils tombent tous avec la même vitesse (abstraction faite de la résistance de l'air). On le constate facilement en laissant tomber en même temps, dans un long tube où on a fait le vide, des objets les plus divers: ils parviennent tous en même temps au bas du tube.

Une tonne de plomb ou une feuille de papier lâchés ensemble du haut d'une tour dans le vide atteignent le sol simultanément, avec une vitesse dont l'accélération, est de 981 centimètres par seconde.

C'est un fait que Lucrèce connaissait déjà. Voici en effet ce qu'écrivait il y a deux mille ans l'immortel et profond poète:

[124] Si la pesanteur était une force analogue à l'attraction électrique, à la traction d'une locomotive, ou bien à l'action propulsive d'une charge de poudre, il ne devrait pas en être ainsi. Les vitesses qu'elle imprime à des masses disparates devraient être différentes. Les deux trains inégalement massifs de notre exemple précédent reçoivent des accélérations inégales sous l'impulsion de la même locomotive. Pourtant, si subitement une fosse profonde s'ouvrait sous eux, ils y tomberaient avec la même vitesse.

De là à penser que la gravitation n'est pas une force comme le voulait Newton, mais simplement une propriété de l'espace dans lequel se meuvent librement les corps, il n'y a qu'un pas. Einstein le franchit sans hésitation.

Imaginons dans un colossal gratte-ciel un ascenseur dont le câble de retenue soudain se rompt. L'ascenseur va tomber d'un mouvement accéléré, moins vite cependant qu'il ne ferait dans le vide, à cause de la résistance de l'air et du frottement de la cage de l'appareil. Mais imaginons par surcroît que la machine électrique qui actionne l'ascenseur ait, du même coup, son commutateur inversé, et accélère la chute de telle sorte que la vitesse descendante s'accroisse chaque seconde de 981 centimètres. Réaliser cela ne serait qu'un jeu pour les ingénieurs, bien que l'intérêt de cette expérience n'ait pas, jusqu'aujourd'hui, paru assez évident pour la justifier. Mais pourquoi n'aurions-nous pas le droit, [125] de nous écrier parfois comme le poète, lorsqu'il s'agit de clarifier un sujet,

Voici donc notre rêve réalisé, et l'ascenseur tombe de très haut avec précisément la vitesse accélérée d'un objet lâché librement dans le vide.

Si les passagers ont gardé dans cette chute vertigineuse assez de sang-froid pour observer ce qui arrive, ils remarqueront que leurs pieds cessent de presser sur le plancher de l'appareil. Ils pourront soudain se croire semblables à la charmante et poétique princesse de La Fontaine

Les porte-monnaie de nos passagers, même s'ils sont pleins d'or, cesseront de peser dans leurs poches,—ce qui pourra leur causer un moment d'émotion. Leurs chapeaux, s'ils leur échappent des mains, resteront suspendus dans l'air à côté d'eux. Se sont-ils précautionnés d'une balance? Ils observeront que les plateaux restent en équilibre, même si on y pose des poids très différents. Tout cela parce que ces objets tombent vers le sol, par l'effet naturel de la pesanteur, avec la même vitesse que l'ascenseur lui-même. La pesanteur en a disparu.

[126]

Jules Verne avait déjà décrit des effets semblables dans l'obus qui porte ses héros de la Terre à la Lune et au moment où le romanesque projectile arrive au «point neutre», à l'endroit où, échappant à l'attraction terrestre, il ne subit pas encore celle de la Lune. Le bon Jules Verne a d'ailleurs commis quelques petites hérésies scientifiques au sujet de cet obus. Il a particulièrement oublié que—en vertu même du principe d'inertie dans ce qu'il a de plus grossièrement évident—les infortunés voyageurs devaient être aplatis comme galette, contre le culot de l'obus, à l'instant du départ du coup. Il a cru aussi, bien à tort, que les objets cessaient de peser dans l'obus seulement à l'instant où il passe exactement entre les deux sphères d'attraction terrestre et lunaire.

Passons sur ces vétilles du romancier et revenons à l'image excellente qu'il nous a prophétiquement fournie pour la commodité de notre exposé einsteinien.

Considérons donc le projectile lorsqu'il commence à tomber librement vers la Lune[8]. Il est évident qu'à [127] partir de cet instant et jusqu'à ce qu'il ait atterri ou plutôt aluni..., il se comportera exactement comme notre ascenseur—je devrais dire notre descenseur—de tout à l'heure.

Pendant cette chute vers la Lune, les passagers—miraculeusement échappés à l'aplatissement fatal du départ—verront tous les objets autour d'eux soudain démunis de leur poids rester suspendus en l'air, et, sous l'influence de la moindre chiquenaude, aller se coller aux parois ou à la voûte ogivale de l'obus. Eux-mêmes se sentiront d'une extraordinaire légèreté et sans effort feront les bonds les plus prodigieux, à rendre jaloux Nijinski.

C'est qu'eux-mêmes et tous les objets voisins tombent vers la Lune avec la même vitesse que l'obus. D'où pour eux disparition de la pesanteur, de la gravitation, soudain subtilisées comme par un magicien. Le magicien, c'est le mouvement accéléré comme il convient, c'est la chute libre des observateurs.

En résumé, pour supprimer en un lieu quelconque les effets apparents de la gravitation, il suffit que l'observateur possède une vitesse convenablement accélérée. C'est ce qu'Einstein appelle le «principe d'équivalence»: équivalence des effets de la pesanteur et de ceux d'un mouvement accéléré.

L'un et l'autre sont indiscernables.

Supposons notre obus de Jules Verne et ses infortunés passagers transportés très loin de la Lune, de la Terre et du Soleil même, en un de ces endroits [128] déserts et glacés de la Voie Lactée où n'existe aucune matière, et si éloigné de toutes les étoiles qu'il n'y a plus là pesanteur ni attraction, et que notre obus abandonné y restera immobile. Dans ces conjonctures, cela est clair, il n'y aura ni haut, ni bas, ni pesanteur pour les passagers de l'obus. Ils se trouveront débarrassés et allégés de toutes les contingences du poids. Ils pourront indifféremment se mettre debout sur la paroi interne du sommet de l'obus ou sur son culot, comme ce fut durant qu'ils tombaient vers la Lune.

Imaginons maintenant que l'Enchanteur Merlin survienne subrepticement puis, ayant attaché une corde à l'anneau extérieur qui surmonte le projectile, se mette à le tirer d'un mouvement uniformément accéléré. Que se passe-t-il alors pour les passagers? Ils remarquent soudain qu'ils ont retrouvé leur poids et qu'ils sont rivés au plancher de l'obus, à peu près comme, avant leur voyage, ils étaient fixés au sol de notre planète terraquée. Si même le mouvement de l'Enchanteur Merlin s'accélère de 981 centimètres par seconde, ils éprouveront exactement les mêmes sensations pesantes que sur la Terre.

Ils remarqueront que si, à un moment donné, ils lâchent en l'air une assiette, elle tombera sur le plancher et s'y brisera. «C'est, penseront-ils, parce que nous sommes de nouveau soumis à la pesanteur; cette assiette tombe en vertu de son poids, de sa masse pesante.» Mais l'Enchanteur Merlin dira lui: «Cette assiette tombe parce qu'elle a gardé, en vertu de son inertie, [129] de sa masse inerte, la vitesse ascendante qu'elle possédait au moment qu'on l'a lâchée. Aussitôt après, puisque je tire l'obus d'un mouvement accéléré, la vitesse ascendante de celui-ci a dépassé celle de l'assiette lâchée. C'est pourquoi le fond de l'obus, dans sa course ascendante accélérée est venu heurter l'assiette et la briser.»

Ceci prouve que le poids d'un corps, sa gravitation, est indiscernable de son inertie. Masse inerte, masse pesante sont deux choses, non pas égales par une extraordinaire coïncidence comme le croyait Newton, mais identiques et inséparables. Ces deux choses n'en sont qu'une.

Et alors nous sommes amenés à penser que les lois de la pesanteur et celles de l'inertie, les lois de la gravitation et celles de la mécanique doivent être identiques, ou du moins doivent être des modalités d'une chose unique. Pareillement la face et le profil d'un même visage ne sont que ce même visage vu sous deux angles différents.

Si même les voyageurs de notre obus—qui sont vraiment des sortes de cobayes!—mettent l'œil au hublot et voient la corde qui les remorque, leur illusion persistera. Ils se croiront suspendus et immobiles en un point de l'espace où la pesanteur est ressuscitée, c'est-à-dire, comme disent les spécialistes, en un point de l'espace où règne un «champ de gravitation».

Cette locution est analogue à l'expression courante de «champ magnétique» qui désigne une région de [130] l'espace où s'exercent des actions magnétiques, où la boussole se voit imposer une orientation.

En résumé, on peut en tout lieu remplacer un champ de gravitation, remplacer l'effet de la pesanteur par un mouvement convenablement accéléré de l'observateur et réciproquement. Il y a équivalence complète entre les effets de la pesanteur et ceux d'un mouvement approprié.

Ceci va nous permettre d'établir maintenant, avec beaucoup de simplicité, ce fait fondamental qu'on ne soupçonnait pas il y a quelques années et qui a été brillamment démontré par l'expérience: la lumière ne se propage pas en ligne droite dans les parties de l'Univers où il y a de la gravitation, mais sa trajectoire est incurvée comme celle des objets pesants.

Nous avons établi au cours d'un précédent chapitre que dans le continuum à quatre dimensions où nous vivons, que l'on pourrait appeler l'espace-temps, et que nous appellerons plus simplement l'Univers, il y a quelque chose qui reste constant, et identique pour des observateurs se déplaçant à des vitesses données et différentes. C'est l'«Intervalle» des événements.

Il est naturel de penser que cet «Intervalle» restera identique même si la vitesse de l'observateur varie, même si elle est accélérée comme celle de notre ascenseur ou de l'obus de Jules Verne pendant leur chute.

[131] En effet si, pour deux observateurs se déplaçant à des vitesses différentes, quelque chose dans l'Univers est un invariant comme disent les physiciens, c'est-à-dire est invariable, ce quelque chose doit naturellement rester tel pour un troisième observateur dont la vitesse passe graduellement de celle du premier à celle du second, et qui, par conséquent, est animé d'un mouvement uniformément accéléré.

Des conséquences fondamentales en découlent.

Une chose d'abord est évidente, admise d'un consentement unanime par tous les physiciens: c'est que dans le vide, et en un point de l'espace où ne s'exerce aucune force et où il n'y a pas de pesanteur, la lumière se propage en ligne droite. Cela est certain pour beaucoup de motifs et d'abord par pure raison de symétrie, parce qu'en une région du vide isotrope, un rayon que rien ne sollicite ne doit point dévier de sa marche rectiligne, dans un sens ou dans l'autre. Cela est évident quelque hypothèse qu'on fasse sur la nature de la lumière, et même si, comme Newton, on suppose qu'elle est formée de particules pesantes.

Ceci admis, supposons maintenant qu'en un point de l'Univers où il y a de la pesanteur, à la surface de la Lune, par exemple, un merveilleux fusil puisse tirer une balle qui possède et garde (tout le long de la trajectoire) la vitesse de la lumière.

Cette balle décrira une trajectoire très tendue, à cause de sa grande vitesse, et néanmoins incurvée vers le sol lunaire, à cause de la pesanteur. Puisque nous pouvons [132] cueillir à loisir dans le champ des hypothèses, rien ne nous empêche de supposer que cette balle est une balle traçante qui marque sa trajectoire par une légère traînée lumineuse. La grande guerre a connu des balles de ce genre.

Cette balle, en même temps qu'elle avance, tombe chaque seconde vers le sol lunaire, d'une quantité égale à celle dont tomberait tout autre projectile lancé à n'importe quelle vitesse, ou même sans vitesse. Tous les objets près de la surface du sol tombent (dans le vide) avec la même vitesse verticale, et qui est indépendante de leur déplacement dans le sens horizontal. C'est même pour cela que les trajectoires des projectiles sont d'autant plus incurvées qu'ils ont une plus faible vitesse initiale.

Observée à travers les hublots de l'obus de Jules Verne (qui, au même moment, tombe librement vers la Lune), la trajectoire de cette balle paraîtra aux passagers une ligne droite parce qu'elle tombe avec la même vitesse qu'eux.

Supposons qu'un rayon lumineux provenant de la lueur du fusil sorte de celui-ci en même temps que la balle, en la rasant, et dans la même direction. Ce rayon lumineux sera évidemment rectiligne pour les passagers de l'obus, puisque la lumière se propage en ligne droite quand il n'y a pas de pesanteur. Par conséquent, puisqu'il a la même forme, la même direction et la même vitesse que la balle fusante, les passagers verront ce rayon lumineux coïncider pendant tout son trajet avec la trajectoire de cette balle.

[133] Par conséquent encore, l' «Intervalle» (à la fois dans le temps et dans l'espace) du rayon lumineux et de la balle est et reste zéro. Or cet «Intervalle» doit demeurer tel, quelle que soit la vitesse de l'observateur. Si donc l'obus de Jules Verne ne tombe plus mais est arrêté à la surface de la Lune, ses passagers continueront de voir le rayon lumineux coïncider en chacun de ses points, avec la trajectoire de la balle. Cette trajectoire (ils le remarquent maintenant) est incurvée par la pesanteur; donc le rayon lumineux est pareillement incurvé par elle.

Ceci démontre que la lumière ne se propage pas en ligne droite mais tombe exactement comme tous les objets, sous l'influence de la gravitation.

Si on ne l'a jamais constaté naguère, si on a toujours cru que la lumière se propage en ligne droite, c'est que par suite de son énorme vitesse, sa trajectoire n'est que très peu courbée par la pesanteur.

Cela est compréhensible. A la surface de la Terre par exemple, la lumière doit tomber (comme tous les objets) avec une vitesse qui au bout d'une seconde est de 981 centimètres. Or, au bout d'une seconde, un rayon lumineux a déjà parcouru 300 000 kilomètres. Supposons (ce qui est bien exagéré) qu'on puisse observer près de la surface de la Terre un rayon lumineux horizontal de 300 kilomètres de long. Pendant le millième de seconde que ce rayon emploiera à aller d'un observateur à l'autre il tombera seulement d'une quantité égale à 5 millièmes de millimètre.

On conçoit qu'un rayon lumineux qui, sur une distance [134] de 300 kilomètres, ne s'éloigne de sa direction initiale que de cette quantité absolument inobservable, ait toujours été considéré comme rectiligne.

N'est-il donc nul moyen de vérifier si, oui ou non, la lumière est incurvée par la gravitation?

Ce moyen existe et c'est l'astronomie qui va nous l'apporter.

S'il est impossible d'apprécier la courbure d'un rayon lumineux allant d'un point à l'autre de la surface terrestre, c'est d'abord parce que la pesanteur sur la Terre est trop petite pour infléchir beaucoup ce rayon; c'est ensuite parce que nous ne pouvons pas le suivre sur une suffisante distance, notre planète étant ridiculement petite.

Mais ce qu'on ne peut faire sur ce petit globule terraqué, dont la lumière rapide franchit le diamètre tout entier en un vingt-cinquième de seconde, on arrivera peut-être à le réaliser dans le laboratoire gigantesque de l'espace céleste. Justement nous avons, presque à portée de la main,—à 150 millions de kilomètres, seulement, d'ici—un astre sur lequel la pesanteur est vingt-sept fois plus intense qu'ici-bas. C'est le Soleil. Un corps abandonné à lui-même y tombe dans la première seconde de 132 mètres. Sa chute est vingt-sept fois plus rapide que sur la Terre.

La lumière sera donc, près du Soleil, infléchie beaucoup [135] plus par la pesanteur. Cette inflexion sera encore accrue par le fait que le Soleil a un million et demi de kilomètres de diamètre, et qu'un rayon lumineux a besoin de beaucoup plus de temps pour franchir cette distance que pour franchir le diamètre terrestre. L'action de la pesanteur sur ce rayon s'exerce donc pendant bien plus longtemps que sur un rayon rasant la Terre, et, pour cela aussi, elle l'incurvera davantage.

Soit un rayon lumineux provenant, par exemple, d'une étoile située très loin derrière le Soleil. S'il nous arrive après avoir rasé celui-ci, il se comportera comme un projectile. Sa trajectoire cesse d'être rectiligne, elle est légèrement courbée vers le Soleil. Autrement dit, ce rayon est dévié de la ligne droite, et la direction qu'il a lorsque nos yeux le reçoivent sur la Terre est un peu différente de la direction qu'il possédait en partant de l'étoile. Il a subi une déviation.

Le calcul montre que cette déviation, bien que faible encore, est mesurable. Elle est égale à un angle d'une seconde et trois quarts, angle que les méthodes précises des astronomes permettent de mesurer.

Ah! ça n'est point qu'il soit bien grand cet angle, qu'on en juge: il faut juxtaposer 324 000 angles d'une seconde pour faire un angle droit. Autrement dit, un angle d'une seconde est celui sous lequel on verrait, à 206 kilomètres de distance, les deux extrémités d'un piquet d'un mètre fiché dans le sol. Si nos yeux étaient assez aigus pour voir un homme de taille normale debout à 200 kilomètres de l'endroit où nous nous tenons, [136] notre regard, en fixant successivement sa tête, puis ses pieds, dévierait d'un angle fort petit. Eh bien, cet angle représente exactement la déviation subie par la lumière qui nous vient d'une étoile après qu'elle a rasé le globe d'or du Soleil.

Si minuscule que soit cet angle, les astronomes savent le déterminer grâce à la délicate exactitude de leurs méthodes. Il ne faut point le mépriser, cet angle infime. Il ne faut point dédaigner ceux qui raffinent jusqu'à observer de pareilles bagatelles, puisque aujourd'hui la science en est bouleversée. Einstein a raison contre Newton parce qu'on a pu mesurer cet angle si petit, parce que cette déviation a été constatée en fait.

Pour vérifier si elle existe, une grosse difficulté se présentait.

Comment apercevoir le rayon qui nous vient d'une étoile en rasant le bord du Soleil, c'est-à-dire en plein jour? C'est impossible. Même avec les lunettes les plus puissantes, l'image des étoiles situées à l'arrière-plan du Soleil sont complètement noyées dans l'éclat de celui-ci, ou—pour s'exprimer plus exactement—dans la lumière diffusée par notre atmosphère.

On peut même remarquer à ce propos (si l'on ose ouvrir ici une parenthèse... et pourquoi n'oserait-on pas?) que la nuit nous a appris beaucoup plus de choses que le jour sur les mystères de l'Univers. Dans le symbolisme littéraire, et dans le politique, la lumière du jour est l'image du progrès et du savoir, la nuit l'emblème de l'ignorance. Quelle sottise! C'est blasphémer [137] la nuit dont nous devons vénérer la brune douceur. Et je n'entends point parler ici de son charme romanesque, mais seulement des admirables progrès que nous lui devons dans le savoir.

Minuit n'est pas seulement l'heure des crimes. C'est celle aussi des vastes envolées vers les mondes lointains. Le jour on ne voit qu'un Soleil, la nuit nous en montre des millions. Et si le rideau éblouissant que la lumière solaire étend devant le ciel est tissé de rayons éclatants, c'est un rideau quand même, car il nous rend pareils aux phalènes qu'une lumière trop vive empêche de voir plus loin que le bout... de leurs ailes.

Il faut donc, pour résoudre notre problème, voir en pleine nuit des étoiles dont l'image serait près du bord solaire. Cela est-il donc impossible? Non. La nature y a pourvu en créant des éclipses totales de soleil, visibles parfois en certains lieux de la Terre.

Alors, et pendant quelques minutes, le disque radieux est très exactement caché derrière celui de la Lune, si bien qu'en plein jour tout se passe comme s'il était nuit, et qu'on voit les étoiles briller près du Soleil masqué de noir.

Tout justement, une éclipse totale devait être visible en Afrique et dans l'Amérique du Sud le 29 mai 1919, peu après qu'Einstein eut, par un raisonnement semblable [138] à celui qui précède, annoncé la déviation des rayons stellaires près du soleil.

Deux expéditions furent organisées par les astronomes de Greenwich et d'Oxford. L'une s'installa à Sobral au Brésil, l'autre dans une petite île portugaise, Principe, dans le golfe de Guinée.

Certains des astronomes anglais étaient bien un peu sceptiques sur le résultat. Comment admettre, jusqu'à preuve du contraire, que Newton s'est trompé, ou du moins n'a pas donné une loi parfaite? Cette preuve du contraire résulta pourtant, et d'éclatante façon, des observations faites.

Celles-ci consistèrent à photographier sur un certain nombre de plaques, et pendant les quelques minutes de l'éclipse totale, les étoiles voisines du Soleil occulté. Elles avaient été, avec les mêmes lunettes, photographiées quelques semaines auparavant, alors que la région du ciel où elles brillent était encore dans la nuit et loin du Soleil. Celui-ci comme on sait, traverse successivement, dans sa course annuelle, les diverses constellations du Zodiaque.

Si la lumière des étoiles photographiées n'était pas déviée en passant près du Soleil, il est évident que leurs écartements devaient être identiques sur les plaques prises pendant l'éclipse et sur les plaques prises la nuit, quelque temps auparavant.

Mais si leur lumière était déviée pendant l'éclipse, par l'attraction du Soleil, il en devait être tout autrement. Voici pourquoi: Quand la Lune se lève sur une de nos [139] plaines, elle n'est pas ronde, tout le monde l'a remarqué, mais aplatie dans le sens vertical et semblable un peu à une gigantesque mandarine posée sur l'horizon, pour je ne sais quel souper fantasmagorique. Pourtant la Lune n'a pas cessé d'être ronde. Si elle semble aplatie, c'est parce que les rayons provenant de son bord inférieur, et qui nous arrivent après avoir traversé une couche d'air très épaisse, sont courbés vers le sol par la réfraction de cette couche d'air, et bien plus que les rayons du bord supérieur qui traversent une moindre épaisseur d'atmosphère. Notre œil voit le bord lunaire dans la direction suivant laquelle nous arrivent ses rayons et non pas dans celle où ils sont partis. C'est pourquoi le bord inférieur de la Lune nous paraît surélevé sur l'horizon plus qu'il n'est réellement. Cette déviation est due à la réfraction.

Semblablement, une étoile située un peu à l'Est du Soleil (et dont la lumière est courbée, non point par la réfraction, mais par la pesanteur) nous paraîtra plus écartée de lui. Elle nous paraîtra plus à l'Est qu'elle n'est en réalité. De même une étoile située à l'Ouest du Soleil nous paraîtra décalée vers l'Ouest du bord solaire occidental.

Donc les étoiles situées de part et d'autre du Soleil paraîtront plus écartées, plus séparées les unes des autres sur les clichés pris pendant l'éclipse. Dans leur position normale, sur les clichés pris pendant la nuit, elles sembleront au contraire plus resserrées, plus rapprochées.

[140] C'est précisément ce qu'on a constaté, par l'étude micrométrique des photographies obtenues à Sobral et à Principe. Non seulement la déviation de la lumière des étoiles par le Soleil a été ainsi démontrée, mais on a constaté que cette déviation a exactement la grandeur numérique annoncée par Einstein. Elle correspond à un angle d'une seconde et trois quarts (1"75) pour une étoile tangente au bord solaire, angle qui décroît proportionnellement très vite pour des étoiles plus éloignées de ce bord. Glorieux triomphe de la théorie et qui établissait pour la première fois un lien entre la lumière et la gravitation!

J'ai comparé il y a un instant l'incurvation de la lumière par la pesanteur à celle que produit la réfraction atmosphérique. Précisément certains astronomes se sont demandé si la concordance de la théorie d'Einstein et des résultats obtenus pendant l'éclipse était autre chose qu'une coïncidence, et si les déviations observées ne provenaient pas d'une réfraction causée dans l'atmosphère du Soleil.

Cette explication paraît insoutenable. On observe parfois des comètes traversant l'espace tout près de la surface solaire. Elles subissent dans leur mouvement une résistance qui le perturberait complètement si le Soleil avait une atmosphère assez réfringente pour expliquer les déviations observées à Sobral et à Principe. De telles perturbations des orbites cométaires près du Soleil n'ont jamais été constatées. Cela exclut [141] toute autre interprétation qu'un effet de la pesanteur sur la lumière.

Ainsi, les rayons des étoiles pesés par des procédés d'une exquise délicatesse, ont fourni l'éclatante confirmation des prémisses théoriques d'Einstein.

A ses fruits on juge l'arbre.

On enseigne toute une magnifique série de théorèmes de géométrie solidement emboîtés les uns dans les autres et dont les principaux furent autrefois créés par un grand génie grec, Euclide. C'est pourquoi cette géométrie classique s'appelle la géométrie euclidienne. [143] Ces théorèmes sont basés sur un certain nombre d'axiomes et de postulats qui ne sont, en somme, que des affirmations, des définitions.

La principale de ces définitions est la suivante: La ligne droite est le plus court chemin d'un point à un autre. Cela paraît tout simple aux écoliers parce qu'ils savent qu'au stade le coureur qui s'amuse à faire des zigzags arrivera au but après les autres... et quand on va souvent au terrain de sports on n'a ni l'envie, ni le loisir de se dessécher sur la validité des axiomes de la géométrie. Que veut dire exactement cette définition de la ligne droite? On en a longtemps discuté et Henri Poincaré a écrit là-dessus des pages profondes et fines, mais dont la conclusion n'est pas dénuée d'un peu d'incertitude.

Dans la pratique, chacun de nous sait bien ce qu'il appelle une ligne droite: c'est la ligne que dessine l'arête d'une règle bien dressée. Comment sait-on qu'une règle est bien dressée? En la plaçant devant l'œil et en observant que ses deux extrémités, lorsqu'on les vise, sont confondues par le regard qui voit en même temps tous les points intermédiaires de l'arête. C'est comme cela que les menuisiers jugent qu'une planche est rabotée droit. En un mot nous appelons ligne droite, dans la pratique, la ligne que suit le regard du tireur entre le guidon et le cran de mire.

Tout cela revient en somme à définir la ligne droite par la direction d'un rayon lumineux.

Comme qu'on retourne la question on en arrive [144] toujours à ceci: dire que le bord d'un objet est droit, c'est dire que la ligne qui le délimite coïncide sur toute sa longueur avec un rayon lumineux[9]. On peut donc affirmer: pratiquement la ligne droite est le chemin parcouru par la lumière dans un milieu homogène.

Mais alors une question se pose. Le monde où nous vivons, l'univers est-il conforme à la géométrie d'Euclide, est-il euclidien, pour employer l'adjectif à la mode qui n'est peut-être pas encore au dictionnaire de l'Académie, mais qui y sera?

Car il faut bien dire maintenant que la géométrie d'Euclide n'est pas la seule qu'on ait créée. Au xix^e siècle des savants profonds et hardis, Riemann, Bolyay, Lobatchewski, Poincaré lui-même, ont fondé des géométries nouvelles très différentes, assez étranges. Elles sont tout aussi logiques et cohérentes que la géométrie classique d'Euclide, mais elles sont basées sur des axiomes, sur des postulats autres, c'est-à-dire sur des définitions différentes.

Par exemple on appelle parallèles deux lignes droites situées dans un même plan et qui ne se rencontrent jamais. La géométrie chère à notre enfance dit: par un point on ne peut faire passer qu'une seule parallèle à une droite donnée. C'est ce qu'on appelle le postulat d'Euclide. Survient Riemann qui n'admet pas ce postulat et le remplace par celui-ci: par un point on [145] ne peut faire passer aucune droite parallèle à une droite donnée, c'est-à-dire aucune ligne qui ne la rencontre jamais. Et là-dessus il fonde une géométrie parfaitement cohérente.

Qui oserait affirmer que la géométrie d'Euclide est vraie, celle de Riemann fausse? Comme constructions théoriques idéales, elles sont aussi vraies l'une que l'autre.

On peut poser la question suivante: le monde réel correspond-il à la géométrie classique d'Euclide ou à celle de Riemann?

On a cru longtemps qu'il correspondait à la géométrie d'Euclide. Poincaré lui-même disait, parlant de celle-ci: «Elle est et restera la plus commode: 1^o parce qu'elle est la plus simple; 2^o parce qu'elle s'accorde assez bien avec les propriétés des solides naturels, ces corps dont se rapprochent nos membres et notre œil et avec lesquels nous faisons nos instruments de mesure.»

Lorsque les anciens affirmaient que la Terre est plate, ils assuraient de même... ou à peu près: «Cette notion est la plus commode: 1^o parce qu'elle est la plus simple; 2^o parce qu'elle s'accorde assez bien avec les propriétés des objets naturels avec lesquels nous sommes en contact.» Mais quand les hommes sont venus en contact avec des objets plus éloignés, quand les navigateurs et les astronomes ont multiplié ces [146] objets nouveaux, la notion de la Terre plate a cessé d'être la plus commode, la plus simple, la mieux adéquate aux données sensibles. Et alors a surgi la notion de la rotondité de la Terre qui s'est trouvée infiniment plus commode, plus simple, mieux adaptée au monde extérieur.

La commodité, qui est pour Poincaré le criterium de la vérité scientifique, est une chose contingente et élastique. Tel point de vue est commode à Paris, qui ne le sera plus à Pontoise. Telle théorie est commode sur un espace de 100 mètres qui ne le sera plus sur un espace de 100 millions de kilomètres.

L'hypothèse d'une Terre plate a cédé le pas à celle d'une Terre ronde. La Terre immobile a cédé le pas à la Terre tournante. De même il semble qu'aujourd'hui, la géométrie euclidienne doive céder le pas à une autre, comme représentation commode du monde réel.

Dans l'Univers, dans notre espace réel peut-on mener une parallèle à une droite? C'est-à-dire deux droites réelles situées dans le même plan peuvent-elles ne jamais se rencontrer? Cette question signifie ceci: deux rayons lumineux cheminant dans l'espace vide et dans ce que (pour chaque fraction de ces rayons) nous appellerons un même plan, peuvent-ils ne jamais se rencontrer? La réponse à cette question est non.

Puisque dans l'espace céleste ces deux rayons lumineux sont déviés par la gravitation des astres, puisque d'ailleurs ils sont déviés inégalement, leur distance à ces astres étant différente, il s'ensuit nécessairement [147] qu'ils cessent d'être parallèles (au sens euclidien du mot) et qu'ils finissent par se rencontrer; ou bien qu'ils cessent de remplir la première condition du parallélisme: la coexistence dans un même plan local.

En un mot, et pourvu qu'on le considère non plus dans le champ ridiculement borné des expériences de laboratoire, mais dans le vaste champ des étendues célestes, l'univers réel n'est pas euclidien parce que la lumière ne s'y propage pas en ligne droite.

Kant considérait les vérités, ou, pour mieux dire, les affirmations déductives de la géométrie euclidienne, comme des «jugements synthétiques a priori», comme des évidences sans autre issue qu'elles-mêmes. Nous venons de voir que là-dessus Kant s'est trompé, non seulement du point de vue de la géométrie théorique, mais aussi du point de vue de la géométrie réelle. L'étymologie seule du mot géométrie, qui signifie mesure du terrain, suffit d'ailleurs à montrer qu'elle fut à l'origine, et avant tout, une science pratique. Cela légitime assez la question que nous avons posée ici, de savoir à quelle géométrie s'apparente l'Univers réel.

Gauss, ce profond esprit, s'était déjà posé la question et il avait, au siècle passé, tenté des expériences précises pour mesurer si la somme des angles d'un triangle est égale à deux droits comme l'affirme la géométrie euclidienne. Dans ce dessein, il forma un vaste triangle dont les sommets étaient constitués par les points culminants de trois montagnes éloignées. L'une était le célèbre Brocken. Il fit, avec ses aides, simultanément [148] des visées de chacun des sommets aux deux autres. Il trouva que la somme des trois angles du triangle ne différait de 180 degrés que d'une quantité égale aux erreurs d'expérience.

Beaucoup de béotiens et quelques philosophes se moquèrent fort de ces expériences et de Gauss. Ils déclarèrent, avec le catégorisme apriorique qu'on rencontre parfois chez les uns et les autres, que les mesures même si elles avaient eu un autre résultat n'auraient rien prouvé contre les théorèmes d'Euclide, mais établi seulement que quelque cause perturbatrice incurvait les rayons lumineux entre les trois sommets du triangle. C'est exact, mais cela ne signifie rien.

Si Gauss avait trouvé que la somme des angles du triangle étudié dépassait deux droits, cela aurait prouvé que la géométrie réelle n'était pas celle d'Euclide. La question que s'était posée Gauss était pleine de profondeur et de sens. Les béotiens et quelques philosophes qui le conspuèrent eussent pu être mis au défi de définir les lignes droites réelles, les lignes droites naturelles autrement que par les trajets de la lumière.

Si Gauss n'a pas trouvé que la somme des angles fût différente de deux droits c'est parce que ses mesures étaient trop peu précises. Si elles avaient été beaucoup plus exactes, ou s'il avait pu opérer sur un triangle plus grand, dont les sommets eussent été la Terre, Jupiter en opposition et une autre planète, il eût trouvé une différence notable.

L'Univers réel n'est donc pas euclidien. Il n'est à [149] peu près euclidien que dans les régions de l'espace où la lumière se propage rectilignement, c'est-à-dire aux endroits très éloignés de toute masse gravitante, tel celui où nous avions plus haut abandonné l'obus de Jules Verne.

Bien d'autres raisons encore font que, par suite de la gravitation, l'Univers n'est pas conforme à la géométrie d'Euclide.

Exemple: Dans cette géométrie la longueur de la circonférence est avec son diamètre dans un certain rapport bien connu et qui est désigné par la lettre grecque π. Ce rapport qui exprime combien de fois le diamètre est compris dans la circonférence est égal à 3,14159265... etc... j'en passe car π possède un nombre infini de décimales. Alors voici la question: Dans la pratique, le rapport des circonférences à leurs diamètres est-il réellement égal à la valeur classique de π? Par exemple le rapport de la circonférence de la Terre[10] à son diamètre a-t-il précisément cette valeur? Selon Einstein, la réponse est non, et en voici la preuve: Imaginons que deux géodésiens, deux arpenteurs très habiles, très rapides et un peu magiciens, se proposent de mesurer la circonférence et le diamètre de la Terre à l'Équateur. Ils sont munis de règles graduées identiques. Ils commencent leurs mesures en même temps et en partant du même point de l'Équateur. Seulement [150] l'un se dirige vers l'Ouest, l'autre vers l'Est et leurs vitesses sont égales et telles que celui qui va vers l'Ouest annule en quelque sorte la rotation de la Terre et voit toute la journée le Soleil immobile à la même hauteur au-dessus de l'horizon. Ainsi, dans les music-halls, on voit parfois un jongleur qui, marchant sur une boule en mouvement, reste cependant au sommet de la boule parce que la vitesse de ses pas est exactement égale et contraire au déplacement de la surface sphérique.

Un observateur immobile dans l'espace, par exemple sur le Soleil, verra donc immobile, en face de lui, celui de nos deux arpenteurs qui se dirige vers l'Ouest. Au contraire, celui qui va vers l'Est lui paraîtra tourner autour de la Terre et deux fois plus vite que s'il était resté à son point de départ.

Nos deux arpenteurs lorsqu'ils auront, à la même vitesse, achevé chacun de son côté de mesurer le tour de la Terre, auront-ils trouvé la même longueur? Évidemment non. Car, comme le constate le sur-observateur placé dans le Soleil, le mètre de l'arpenteur qui va à l'Est est raccourci par sa vitesse, en vertu, nous l'avons montré, de la contraction Fitzgerald-Lorentz. Au contraire le mètre de l'arpenteur qui va à l'Ouest ne subit pas cette contraction, ainsi que le constate le sur-observateur solaire, par rapport à qui il est immobile.

Par conséquent les deux arpenteurs trouvent pour le diamètre terrestre des nombres différents, et celui qui se dirige vers l'Ouest trouve un nombre de mètres [151] plus petit que l'autre. D'autre part il est évident que lorsqu'ils mesurent ensuite le diamètre terrestre en le parcourant à la même vitesse, nos deux observateurs trouveront pour ce diamètre deux valeurs identiques.

Le nombre π qui exprime, d'après les mesures faites, le rapport de la circonférence de la Terre à son diamètre, est donc différent, selon qu'on marche dans le sens où la Terre tourne, ou dans le sens inverse. Puisque les valeurs réelles du nombre π sont diverses, c'est donc qu'elles ne peuvent être le nombre unique et bien déterminé de la géométrie classique. C'est donc que l'Univers réel n'est pas conforme à cette géométrie.

Ces différences, dans l'exemple précédent, proviennent de ce que la Terre tourne. Au point de vue de la gravitation, la rotation terrestre a des effets centrifuges qui diminuent l'effet centripète de la pesanteur. Nous venons de voir d'ailleurs que pour celui de nos deux arpenteurs dont la vitesse annule la rotation terrestre, la valeur du nombre π est plus petite que pour l'observateur dont la vitesse semble doubler cette rotation. Les effets de la pesanteur étant inverses de ceux de la rotation, de la force centrifuge, il s'ensuit donc (et la démonstration en est aussi simple que la précédente) que l'effet de la pesanteur est de donner au nombre π une valeur plus petite que sa valeur classique.

En un mot, dans l'Univers les circonférences réelles tracées autour des masses gravitantes, autour des astres, ont par rapport à leur diamètre, une longueur plus petite que dans la géométrie euclidienne.

[152] La différence est d'ailleurs en général assez faible. Mais elle n'est pas nulle. Si on place une masse de 1 000 kilogs au centre d'un cercle de 10 mètres de diamètre, le nombre π différera réellement de sa valeur euclidienne de moins d'un septillionième, c'est-à-dire de moins d'un millionième de milliardième de milliardième.

Au voisinage de masses formidables comme celles des astres, la différence pourra être beaucoup plus grande, ainsi que nous verrons. C'est de là surtout que proviennent les divergences entre la loi de gravitation de Newton et celles d'Einstein, divergences que l'observation a tranchées à l'avantage de celle-ci.... Mais n'anticipons pas....

Nous avons montré dans un chapitre précédent que l'Univers réel des relativistes est un continuum à quatre dimensions et non pas à trois comme le croyait la science classique, et qu'au sein de ce continuum les distances dans l'espace et les distances dans le temps sont relatives. Seul a une valeur indépendante des conditions d'observation, seul a une réalité absolue... ou du moins objective, ce que nous avons appelé l'«Intervalle» des événements, synthèse des données spatiales et chronologiques.

Mais, pour avoir quatre dimensions, l'Univers, tel que nous l'avons discuté à propos de l'expérience de Michelson [153] et de la relativité spéciale qui s'y rattache, n'en était pas moins un continuum euclidien, où la géométrie classique était vérifiée, où la lumière se propageait en ligne droite.

Il faut déchanter, nous venons de le voir. Non seulement il est à quatre dimensions, mais il n'est pas euclidien.

A quelle géométrie s'apparente le mieux, le plus commodément—pour parler comme Poincaré—cet Univers? Probablement à celle de Riemann. Lorsqu'on trace, sur une feuille de papier étalée sur la table, un petit cercle au moyen d'un compas, le rayon de ce cercle est donné par l'écartement des pointes du compas et ce cercle est euclidien. Mais si on trace ce cercle sur un œuf, la pointe fixe du compas étant piquée au sommet de l'œuf, et si le rayon est de nouveau donné par l'écartement des pointes, le cercle tracé n'est plus euclidien. Le rapport de la circonférence décrite au rayon ainsi défini est plus petit que π, exactement comme il est plus petit que π lorsque le cercle est tracé autour d'un astre massif.

Eh bien! il y a la même différence entre l'Univers réel non euclidien et un continuum euclidien, qu'entre notre feuille de papier plane et la surface de notre œuf, à cela près que ces surfaces ont deux dimensions tandis que l'Univers en a quatre.

L'espace à deux dimensions peut être plat comme la feuille de papier ou courbe comme la surface de l'œuf. On peut même, suivant qu'on laisse à plat ou qu'on roule une feuille de papier, faire que la géométrie qui [154] s'applique aux figures tracées sur elle soit ou ne soit pas la géométrie euclidienne. D'une manière tout à fait analogue, l'espace à plus de deux dimensions peut être euclidien ou non.

En fait l'Univers, nous venons de le voir, n'est à peu près euclidien que dans les régions du monde très éloignées de toutes masses pesantes. Il n'est pas euclidien mais courbe au voisinage des astres et d'autant plus qu'on en est plus près.

La géométrie de l'espace courbe, telle que l'a fondée Riemann, est donc celle qui paraît le mieux s'appliquer à l'Univers réel. C'est elle qu'Einstein a employée dans ses calculs.

Pour démontrer tout à l'heure que les rayons lumineux tombent comme feraient des projectiles d'égale vitesse, nous sommes partis du raisonnement que voici:

Puisque l'«Intervalle» de deux événements est le même pour deux observateurs animés de vitesses uniformes et différentes, il est naturel de penser qu'il restera le même pour un troisième observateur dont la vitesse passe progressivement de celle du premier à celle du second, c'est-à-dire dont la vitesse est uniformément accélérée.

Il n'y a en effet aucune raison pour que les voyageurs d'un train animé d'une vitesse constante de 100 kilomètres à l'heure, par exemple, observent comme ceux [155] d'un autre train faisant 50 kilomètres à l'heure, quelque chose d'«invariant» dans les phénomènes, tandis que cet «invariant» cesserait d'être tel pour les voyageurs d'un troisième train qui passe graduellement de la vitesse du premier train à celle du second. Admettre le contraire serait donner une situation privilégiée, dans l'Univers, aux deux premiers ou à leurs pareils. Or s'il est un domaine qui a eu réellement sa nuit du 4 août, un domaine où les privilèges injustifiés ont été supprimés par la physique nouvelle, c'est bien la contemplation du monde extérieur.

Ce privilège des observateurs en mouvement uniforme serait d'autant moins justifié que, si on va au fond des choses, il est bien difficile de définir exactement un mouvement uniforme.

Dire qu'un train a une vitesse uniforme de 100 kilomètres à l'heure, qu'est-ce que cela veut dire? Cela veut dire que ce train possède cette vitesse par rapport à la voie, par rapport au sol. Mais par rapport à un observateur en ballon, ou qui passe dans un autre train, cette vitesse n'a plus la même valeur et elle peut cesser d'être une vitesse uniforme. Nous ne connaissons que des mouvements relatifs, et pour mieux dire des mouvements relatifs à tel ou tel objet matériel. Selon le choix de cet objet, de ce repère, une même vitesse pourra être uniforme ou accélérée. Finalement on voit qu'il faudrait revenir à l'hypothèse de l'espace absolu de Newton, pour pouvoir dire si une vitesse donnée est réellement uniforme ou accélérée.

[156] Là est la raison profonde pour laquelle l'«Intervalle» einsteinien des choses, quantité invariable, «Invariant», doit rester le même par rapport à tous les observateurs quelles que soient leurs vitesses, et en particulier pour les observateurs animés de vitesses équivalentes, en un lieu donné, aux effets de la gravitation.

Mais alors les déductions que nous avons tirées de l'expérience de Michelson, relativement à l'aspect des phénomènes pour des observateurs en translations uniformes différentes, ne suffisent plus à nous rendre compte de toute la réalité. Elles ont besoin d'être complétées de sorte que l'invariant universel, l'«Intervalle» des choses, reste tel pour un observateur en mouvement quelconque.

Si je traverse une rue à une vitesse inouïe, mais d'un mouvement uniforme, son aspect général, par suite de la contraction due à ma vitesse, pourra être pour moi un peu différent de ce qu'il m'apparaîtrait si j'étais immobile[11]. Les maisons par exemple me paraîtront plus étroites en proportion de leur hauteur. Cependant l'aspect et les proportions générales des objets, seront à peu près les mêmes dans les deux cas, et auront quelque chose de commun. C'est ainsi que les becs de gaz m'apparaîtront plus minces, mais ils seront toujours droits.

Il en sera tout autrement si l'observateur est animé [157] de mouvements variés quelconques, s'il est par exemple un ivrogne, un ivrogne merveilleux capable de tituber à des vitesses prodigieuses. Pour cet ivrogne, la rue qu'il parcourt aura un aspect tout nouveau. Les becs de gaz ne lui paraîtront plus droits, mais gondolés en zigzags qui reproduiront, en sens inverse, les zigzags qu'il décrit en titubant. Cela est si vrai que les caricaturistes ont l'habitude de représenter en lignes follement sinueuses les arbres, lampadaires et maisons vues par un ivrogne.

Notre homme sera d'ailleurs persuadé que les objets ont bien réellement la forme zigzagante qu'il leur voit, et que cette forme change à chacun de ses pas. Essayez de le persuader que c'est lui qui danse et non pas les réverbères; essayez de lui montrer que c'est lui qui ne marche pas droit et non le chien qu'il tient... ou plutôt qui le tient en laisse. Il n'en croira rien, et ma foi, du point de vue de la relativité généralisée, il aura raison ni plus ni moins que vous.

Pourtant il y a quelque chose qui, dans l'aspect du monde doit rester commun à l'ivrogne et au buveur d'eau.

Si l'Univers tout entier était soudain noyé dans une masse de gélatine qui se prenne en gelée, et que l'on torde, comprime, déforme d'une manière quelconque cette masse gélatineuse, il y aurait quelque chose qui resterait pourtant inaltéré dans ce coagulum. Quel est ce quelque chose, quel est le calcul qu'il faut lui appliquer? La réponse à ces questions constituait la dernière [158] étape à franchir par Einstein pour pouvoir établir les équations de la gravitation et de la relativité généralisée.

Ici c'est le génie pénétrant d'Henri Poincaré qui a réellement tracé la voie. Il est d'autant plus nécessaire d'y insister que justice n'a pas été rendue sur ce point à l'illustre savant français.

Si tous les corps de l'Univers venaient à se dilater simultanément et dans la même proportion, nous n'aurions aucun moyen de le savoir. Nos instruments et nous-mêmes étant dilatés pareillement, nous ne nous apercevrions pas de ce formidable événement historique et cosmique, qui ne nous arracherait pas même un instant à nos petites contingences ridicules.

Il y a plus: non seulement les mondes seront indiscernables s'il se modifient de sorte que soit changée l'échelle des longueurs et des temps; mais ils seront encore indiscernables si, à chaque point de l'un, correspond un point et un seul de l'autre et si, à chaque objet, à chaque événement du premier monde, en correspond un de même nature placé précisément au point correspondant du second. Or, les déformations successives et quelconques que l'on fait subir à la masse gélatineuse où nous avons incorporé plus haut et métaphoriquement l'Univers tout entier, nous fournissent précisément des [159] mondes indiscernables à ce point de vue. Poincaré a la gloire d'avoir attiré l'attention là-dessus et montré que la relativité des choses doit être entendue dans ce sens très large.

Le continuum amorphe et déformable, où nous plaçons l'Univers, possède un certain nombre de propriétés exemptes de toute idée de mesure. L'étude de ces propriétés fait l'objet d'une géométrie particulière, d'une géométrie qualitative. Les théorèmes de cette géométrie ont ceci de singulier, qu'ils resteraient vrais même si les figures étaient copiées par un dessinateur malhabile qui altérerait grossièrement toutes les proportions et qui remplacerait les droites par des lignes irrégulières et sinueuses.

Telle est la géométrie que, suivant l'indication géniale de Poincaré, il sied d'appliquer à ce continuum à quatre dimensions et plus ou moins euclidien, selon ses points, qu'est l'Univers einsteinien. Cette géométrie est précisément celle qui énonce ce qu'il y a de commun entre les formes particulières des objets vues par notre ivrogne et notre buveur d'eau de tout à l'heure.

C'est dans cette voie, ou plutôt dans une voie parallèle à celle-là, qu'Einstein a finalement obtenu le succès. L'Univers étant un continuum plus ou moins incurvé, il a eu l'idée de lui appliquer la géométrie que Gauss a créée pour l'étude des surfaces à courbure variable et que Riemann a généralisée. C'est au moyen de cette géométrie particulière qu'on a exprimé le fait que l'«Intervalle» des événements est un invariant.

[160] Voici maintenant une image qui, je pense, va nous guider au cœur même du problème de la gravitation et jusqu'à sa solution.

Considérons une surface à courbure variable, par exemple, la surface d'un coin de la France avec ses collines, ses montagnes, ses vallonnements. En parcourant ce pays en tous sens, nous pourrons aller en ligne droite tant que nous sommes en plaine. La ligne droite en plaine unie a ceci de remarquable qu'elle est le chemin le plus court entre deux points. Elle a aussi ceci de particulier qu'elle est, entre ces deux points, seule de son espèce et ayant sa longueur, tandis que l'on peut tracer un très grand nombre de lignes non droites réunissant aussi ces deux points, plus longue que la ligne droite mais toutes d'égale longueur.

Mais nous voici arrivés dans la région des collines. Il nous est maintenant impossible pour passer d'un point à un autre, séparés par une colline, de marcher suivant une ligne droite. Comme que nous fassions, notre trajet sera courbe. Mais parmi les divers chemins possibles qui nous mènent d'un point à l'autre par dessus la colline, il en est un, et un seul en général, qui est plus court que tous les autres, ainsi que nous pouvons le constater avec un cordeau. Ce chemin le plus court, seul de son espèce, est ce qu'on appelle la géodésique de la surface traversée.

[161] Pareillement, pour aller de Lisbonne à New-York, aucun navire ne peut marcher en ligne droite. Tous doivent faire un trajet incurvé, à cause de la rotondité terrestre. Mais parmi les trajets incurvés possibles, il en est un privilégié, plus court que tous les autres, c'est celui qui suit la direction d'un grand cercle de la Terre. Pour aller de Lisbonne à New-York, qui sont pourtant à peu près sur le même parallèle, les vaisseaux se gardent bien de cingler droit vers l'Ouest dans la direction des parallèles. Ils cinglent un peu vers le Nord-Ouest, de façon à arriver à New-York en venant du Nord-Est, et à suivre à peu près un grand cercle terrestre. Sur notre globe, comme sur toutes les sphères, la géodésique, le plus court chemin entre deux points, est l'arc de grand cercle passant par ces deux points.

Ainsi sur toutes les surfaces courbes, on peut, d'un point à un autre, tracer une ligne privilégiée de longueur minima, une géodésique qui est, sur ces surfaces, l'analogue de la ligne droite dans le plan.

Eh! bien l'«Intervalle» de deux points dans l'Univers à quatre dimensions (à un signe algébrique près) représente exactement la géodésique, la ligne de trajet minimum tracée dans l'Univers entre ces deux points. Là où l'Univers est incurvé, cette géodésique est une ligne courbe. Là où l'Univers est à peu près euclidien, elle est une ligne droite.

On me dira à ce propos qu'il est bien difficile de se représenter comme incurvé un espace à trois, et a fortiori à quatre dimensions. J'en conviens. Nous avons vu [162] qu'il est déjà assez difficile de se représenter l'espace à quatre dimensions même s'il n'est pas incurvé.

Qu'est-ce que cela prouve? Il y a dans la nature bien d'autres choses que nous ne pouvons pas nous représenter, c'est-à-dire dont nous ne pouvons pas nous former une image visuelle. Les ondes hertziennes, les rayons X, les ondes ultra-violettes en existent-elles moins parce que nous ne pouvons pas nous les figurer, ou que du moins nous ne le pouvons qu'en leur attribuant une forme visible qui précisément leur manque. Certes, c'est une des faiblesses de l'infirmité humaine que de ne rien concevoir que ce qui est imagé. De là cette tendance qui nous porte à tout visualiser (si j'ose risquer ici ce mot inélégant, mais expressif).

Revenons donc à nos géodésiques. Celles-ci nous pouvons très bien nous les représenter, car elles sont dans l'Univers, en dépit de ses quatre dimensions, des lignes à une seule dimension pareilles à toutes les lignes que nous connaissons.

L'existence des géodésiques, des lignes de plus courte distance, va nous dévoiler avec éclat la liaison qui, dans le monde euclidien de la science classique, n'était pas apparue, entre l'inertie et la pesanteur. De là était né le distinguo newtonien entre le principe d'inertie et la force gravitante.

Pour nous relativistes, ce distinguo n'est maintenant [163] plus nécessaire. Les masses matérielles, comme la lumière, se propagent en ligne droite loin de tout champ de gravitation, et en ligne courbe près des masses gravitantes. Par raison de symétrie, un point matériel libre ne peut suivre dans l'Univers qu'une géodésique.

Si alors on considère que la force gravitante invoquée par Newton n'existe pas—et une telle action à distance est bien hypothétique,—si on considère que dans l'espace vide il n'y a que des objets librement abandonnés à eux-mêmes, on est irrésistiblement amené à l'énoncé suivant qui réunit sous une forme simple ces sœurs autrefois séparées, l'inertie et la pesanteur. Tout mobile abandonné librement à lui-même décrit dans l'Univers une géodésique.

Loin des astres massifs, cette géodésique est une ligne droite parce que l'Univers y est à peu près euclidien. Près des astres elle est une ligne courbe, parce que l'Univers n'y est plus euclidien.

Admirable conception et qui réunit sous une seule règle le principe d'inertie et la loi de la pesanteur! Synthèse éclatante de la mécanique et de la gravitation, par quoi disparaît la sécession qui naguère en faisait des sciences séparées et incommunicantes!

Dans cette théorie hardie et simple, la gravitation n'est plus une force. Si les planètes décrivent des courbes c'est parce que, près du Soleil, comme près de toute concentration de matière, l'Univers est incurvé. Le plus court chemin d'un point à un autre est une ligne qui ne nous paraît droite, pauvres pygmées que nous sommes, [164] que parce que nous la mesurons avec des règles très petites et sur de faibles longueurs. Si nous pouvions suivre cette ligne sur des millions de kilomètres et pendant un temps suffisant, nous la trouverions infléchie.

En somme, et si on veut me permettre une image qui n'est qu'une analogie, les planètes décrivent des courbes parce qu'elles avancent suivant le chemin le plus facile dans un univers incurvé, de même qu'au vélodrome les cyclistes arrivant au virage n'ont pas besoin de tourner leur guidon, mais n'ont qu'à pédaler droit devant eux, la pente incurvée les obligeant à tourner naturellement. Au vélodrome, comme dans le système solaire, la courbure est d'autant plus marquée qu'on est plus près du bord interne de la piste.

Maintenant il ne reste plus qu'à assigner à l'Univers, à l'espace-temps, une courbure telle, en ses divers points, que les géodésiques représentent exactement les trajectoires des planètes et des corps qui tombent, en admettant que la courbure de l'Univers est causée en chaque point par les masses matérielles présentes ou voisines.

Dans ce calcul, il faut tenir compte aussi de ce que l'«Intervalle», c'est-à-dire la portion de géodésique entre deux points très voisins, doit être un invariant quelque soit l'observateur. Il arrivera donc que, pour l'ivrogne titubant que nous avons déjà invoqué, une même géodésique sera une ligne courbe ou même sinueuse alors qu'elle est une ligne droite pour un observateur immobile. La longueur de cette ligne, qu'on la voie droite ou courbe, reste la même.

[165] Tenu compte de tout cela, et grâce à des prodiges d'habileté mathématique dont nous avons suffisamment indiqué l'objet, Einstein arrive à exprimer sous une forme complètement invariante, la loi de gravitation.

En calculant par la loi de Newton l'«Intervalle» de deux événements astronomiques, par exemple de deux chutes successives de bolides sur le Soleil, on trouverait que cet «Intervalle» n'a pas exactement la même valeur pour des observateurs animés de vitesse différentes et quelconques.

Avec la forme nouvelle donnée par Einstein à la loi, cette différence n'existe plus. Les deux lois sont d'ailleurs très peu différentes, et il fallait s'y attendre étant donnée l'exactitude avec laquelle depuis deux siècles la loi de Newton a été vérifiée par les astronomes. Le perfectionnement apporté par Einstein à la loi de Newton revient en somme (si nous voulons employer le vieux langage de l'Univers euclidien), à considérer celle-ci comme exacte, sous la condition que les distances des planètes au Soleil soient mesurées avec un mètre dont la longueur diminue légèrement en se rapprochant du Soleil.

Il est étonnant que Newton et Einstein arrivent à exprimer sous une forme à peu près identique les mouvements des astres gravitants, car leurs points de départs sont extrêmement différents.

[166] Newton part de l'hypothèse de l'espace absolu, des lois expérimentales du mouvement des planètes exprimées dans les lois de Képler, et de l'assimilation de l'attraction gravitationnelle à une force proportionnelle à la masse. Einstein au contraire fait ses calculs en partant des conditions d'invariance que nous avons indiquées. Il procède en quelque sorte du postulat philosophique, du principe, du besoin d'affirmer que les lois de la nature sont invariantes, indépendantes du point de vue, irrélatives, si j'ose dire. Einstein abandonne même l'hypothèse qui attribuait la courbure des trajectoires gravitationnelles à une force attractive distincte.

Pourtant, parti de ce point de vue totalement différent du point de vue newtonien, et au premier abord moins surchargé d'hypothèses, Einstein arrive à une loi de gravitation qui est presque identique à la loi de Newton.

Ce presque a un prodigieux intérêt, car il va nous permettre de vérifier quelle est la loi exacte: celle de Newton ou celle d'Einstein. Si elles conduisent au même résultat tant qu'il s'agit de vitesses faibles relativement à celle de la lumière, les deux lois donnent des résultats un peu divergents lorsqu'il s'agit de vitesses très grandes. Nous avons vu déjà que la lumière elle-même subit, près du Soleil, une déviation exactement conforme à la loi d'Einstein, et que la loi de Newton au contraire ne prévoyait pas telle.

Mais il y a une autre divergence entre les deux lois. D'après celle de Newton, les planètes décrivent autour [167] du Soleil des ellipses qui—si on néglige les petites perturbations dues aux autres planètes—ont une position rigoureusement fixe.

Posons sur une table une tranche de citron coupée dans la longueur du fruit et imaginons que sur la voûte de la vaste salle hémisphérique au milieu de laquelle nous supposons cette table, soient peintes les principales étoiles, les constellations boréales. Notre tranche de citron possède à peu près la forme d'une ellipse, et si nous assimilons le Soleil à un des pépins, elle peut figurer ainsi l'orbite d'une planète dans l'Univers stellaire. La loi de Newton dit que—toutes corrections faites—l'orbite planétaire garde une orientation fixe parmi les étoiles, durant que la planète en parcourt indéfiniment le tour. Cela veut dire que notre tranche de citron reste immobile.

Au contraire, la loi d'Einstein affirme que l'ellipse orbitale tourne avec beaucoup de lenteur parmi les étoiles tandis que la planète la parcourt. Cela veut dire que notre tranche de citron doit tourner légèrement sur la table de manière que les deux sommets du citron ne restent pas en face des mêmes étoiles peintes sur le mur.

Si on calcule, par la loi d'Einstein, la quantité dont doivent tourner ainsi les orbites elliptiques des planètes on trouve que cette quantité est inobservable à cause de sa petitesse, sauf pourtant pour une planète, la plus rapide de toutes, Mercure.

Mercure accomplit une révolution complète autour du [168] Soleil en 88 jours environ, et la loi d'Einstein montre que son orbite doit tourner en même temps d'un petit angle qui au bout d'un siècle monte à 43 secondes d'arc (43"). Si petite qu'elle soit, cette quantité est de celles que les astronomes avec leurs méthodes raffinées mesurent facilement.

Précisément, dès le siècle passé on avait remarqué que, seule de toutes les planètes, Mercure présentait dans son mouvement une petite anomalie inexplicable par la loi de Newton. Le Verrier fit à ce sujet des calculs prodigieux, pensant que cette anomalie pouvait être due à l'attraction d'un astre ignoré, situé entre Mercure et le Soleil. Il espérait ainsi découvrir par le calcul une planète intra-mercurielle de même qu'il avait découvert la planète transuranienne: Neptune.

Mais jamais l'observation ne révéla la planète annoncée et l'anomalie du mouvement de Mercure continua à faire le désespoir des astronomes. Or en quoi consistait cette anomalie? Précisément en une rotation anormale de l'orbite planétaire, rotation qui, d'après les calculs de Le Verrier, est de 43 secondes d'arc par siècle. Exactement le chiffre qu'on déduit, sans aucune hypothèse, de la loi de gravitation d'Einstein!

Il est vrai que d'après les calculs récents de Grossmann, il résulte des observations astronomiques réunies par Newcomb que la valeur effectivement constatée du déplacement séculaire du périhélie de Mercure est, non pas de 43" comme le croyait Le Verrier, mais de 38" tout au plus. L'accord avec le chiffre théorique d'Einstein [169] pour n'être plus parfait (ce qui était bien extraordinaire) n'en est pas moins excellent, et en deçà des incertitudes de l'observation.

La loi d'Einstein a la même exactitude que celle de Newton tant qu'il s'agit de planètes lentes. Mais pour les astres plus rapides dont l'observation permet de connaître le mouvement avec une précision supérieure, la loi de Newton est en défaut, celle d'Einstein triomphe encore.

Ce perfectionnement de ce qu'on croyait parfait—l'œuvre de Newton—est une belle victoire de l'esprit humain.

L'astronomie, la mécanique céleste y gagnent une précision et une puissance prophétique accrues. Sur les ailes triomphales du calcul, nous savons maintenant mieux que naguère suivre et précéder les orbes d'or des astres, par delà les siècles et dans l'espace démesuré.

Il existe encore un autre criterium de la loi gravitationnelle d'Einstein. Si celle-ci est exacte, la durée d'un phénomène donné augmente, selon Einstein, quand le champ de gravitation devient plus intense. Par conséquent, la durée de vibration d'un atome donné doit être plus grande sur le Soleil que sur la Terre. Les longueurs d'onde des raies spectrales d'un même élément chimique doivent être un peu plus grandes dans la lumière solaire, que dans une lumière d'origine terrestre. C'est ce que [170] des expériences récentes tendent à établir. Mais ici la vérification est moins nette que dans le cas de Mercure, car d'autres causes peuvent intervenir pour modifier les longueurs d'onde de la lumière.

Au total, la puissante synthèse qu'Einstein a appelée la théorie de la Relativité généralisée, et dont nous venons d'embrasser très vite les grandes lignes, est vraiment une haute et belle construction mentale en même temps qu'un splendide outil à explorer le mystère des choses.

Savoir, c'est prévoir. Elle prévoit cette théorie, et mieux que ses aînées. Elle joint pour la première fois en un faisceau unique la gravitation et la mécanique. Elle montre comment la matière impose au monde extérieur une courbure dont la gravitation n'est que l'indice, de même que les algues qu'on voit flotter sur la mer ne sont que les signes du courant qui les entraîne.

Quelques modifications qu'elle puisse subir dans l'avenir—car tout dans la science reste à jamais perfectible—elle a manifesté, parmi les lois de la nature, un peu plus de cette harmonie qui naît de l'Unité.

Mais j'en ai dit assez là-dessus, si j'ai pu faire comprendre, ou plutôt faire sentir ces choses, sans m'aider de cette pure lumière que la Géométrie projette sur l'invisible.

Kant—ce grognon génial qui trouvait horriblement monotone de voir tous les ans briller le même soleil et fleurir le même printemps—se fondait sur des considérations métaphysiques pour soutenir que l'espace est infini et partout semé d'astres semblables.

Il est peut-être plus prudent de n'examiner ce problème qu'à l'aide des données récentes de l'observation, en fermant soigneusement l'huis de notre discussion sur [172] cette brouilleuse de cartes qu'est la métaphysique. Aussi bien celle-ci nous obligerait à définir l'espace pur, à convenir que nous n'en savons rien et à douter même s'il existe.

La preuve que nous n'en connaissons pas grand'chose est que les newtoniens y croient tandis que les einsteiniens ne le conçoivent que comme un attribut inséparable des objets. Ils définissent l'espace par la matière; il leur faut alors définir celle-ci. Descartes au contraire définissait la matière par l'étendue, c'est-à-dire par l'espace. Cercle vicieux. Le mieux est donc de laisser nettement en dehors de notre exposé les raisonnements métaphysiques de Kant et de nous river éperdûment à l'expérience, à ce qui est mesurable.

Pour simplifier, nous admettrons la réalité de ce continuum où baignent les astres, que parcourent les radiations et que le sens commun appelle l'espace. S'il y avait partout et indéfiniment des étoiles et si le nombre de celles-ci était infini, il y aurait à la fois de l'espace et de la matière partout. Les newtoniens en pourraient triompher comme les einsteiniens, ceux qui croient à l'espace absolu comme ceux qui le nient, les «absolutistes» comme les «relativistes.»

Quel bonheur si les observations astronomiques montraient que le nombre des étoiles est en effet infini, et que par conséquent les tenants des deux opinions contraires peuvent également chanter victoire dans leurs communiqués! Mais que montrent les observations astronomiques?

[173] Certains ont nié a priori que le nombre des étoiles pût être infini. Le nombre des étoiles, disaient-ils, pourrait être augmenté; il n'est donc pas infini puisqu'on ne peut rien ajouter à l'infini. Ce raisonnement est spécieux, mais faux, bien que Voltaire s'y soit laissé prendre. Point n'est besoin d'être grand clerc ès mathématiques pour savoir qu'on peut toujours ajouter à un nombre infini et qu'il existe des quantités infinies qui sont elles-mêmes infiniment petites par rapport à d'autres.

Venons-en donc aux faits.

Si l'Univers des étoiles est sans fin, il n'y a pas une seule ligne visuelle menée de la Terre vers le ciel qui ne doive rencontrer un de ces astres. L'astronome Olbers a remarqué que le ciel nocturne serait alors tout entier d'un éclat comparable à celui du Soleil. Or l'éclat total de toutes les étoiles réunies n'est guère que 3 000 fois celui d'une étoile de première grandeur, c'est-à-dire trente millions de fois plus petit que celui du Soleil.

Mais cela ne prouve rien, car le raisonnement d'Olbers est faux pour deux raisons. D'une part, il y a nécessairement dans le ciel beaucoup d'étoiles éteintes ou obscures. Nous en connaissons qui sont fort bien étudiées et même pesées, et qui manifestent leur existence en venant périodiquement éclipser les étoiles voisines autour desquelles elles tournent. D'autre part, on a découvert depuis peu que l'espace céleste est occupé sur de larges étendues par des masses gazeuses obscures et des nuages de poussière cosmique qui absorbent la lumière des astres situés au delà. On voit bien que l'existence d'un [174] nombre infini d'étoiles est parfaitement compatible avec la faible clarté du ciel nocturne.

Et maintenant, si nous ajustons nos besicles... nos télescopes, veux-je dire, et si nous passons du domaine du possible à celui du réel, les observations astronomiques récentes nous fournissent un certain nombre de faits fort remarquables, et qui conduisent irrésistiblement aux conclusions suivantes.

Le nombre des étoiles n'est pas, comme on l'a cru longtemps, limité par la seule puissance des lunettes. Lorsqu'on s'éloigne du Soleil le nombre des étoiles contenues dans l'unité de volume, la fréquence des étoiles, la densité de la population stellaire, si j'ose dire, ne restent pas uniformes, mais diminuent à mesure qu'on approche des confins de la Voie Lactée.

Celle-ci est un gigantesque archipel d'astres et notre Soleil paraît situé dans sa région centrale. Cet amas, cette fourmilière d'étoiles dont nous faisons partie a grossièrement la forme d'un boîtier de montre dont l'épaisseur serait à peu près la moitié de sa largeur. La lumière qui va en une seconde de la Terre à la Lune, en huit minutes de la Terre au Soleil, en trois ans de la Terre à l'étoile la plus proche, la lumière a besoin d'au moins 30 000 ans, 300 siècles, pour parcourir la Voie Lactée.

[175] Celle-ci contient un nombre d'étoiles compris entre 500 et 1 500 millions. C'est un très petit nombre, au plus égal à celui des êtres humains sur la Terre, et beaucoup plus petit que celui des molécules de fer que renferme une tête d'épingle.

En outre on a découvert des amas très serrés d'étoiles, comme la Nuée de Magellan, l'Amas d'Hercule et divers autres qui ne paraissent guère dépasser les confins de notre Voie Lactée, et sont comme ses faubourgs. Ces faubourgs semblent d'ailleurs s'étendre très loin et surtout d'un côté de la Voie Lactée, et le plus éloigné n'est peut-être pas à moins de 200 000 années de lumière de nous.

Au delà, l'espace paraît désert et privé d'étoiles sur des distances énormes par rapport aux dimensions de notre Univers lacté tel que nous venons de le définir. Mais plus loin encore?

Eh bien! plus loin, on trouve ces astres singuliers, que sont les nébuleuses spirales, posés comme des escargots d'argent dans le jardin des étoiles et dont on a repéré plusieurs centaines de mille. Certains astronomes croient que les amas spiraloïdes d'étoiles sont peut-être des annexes de la Voie Lactée, et des images réduites de celle-ci. Le plus grand nombre incline à penser, par des raisons très fortes, que les nébuleuses spirales sont des systèmes en tout analogues à la Voie Lactée et de dimensions comparables aux siennes.

Dans le premier cas, l'ensemble des astres accessibles à nos télescopes a des dimensions franchissables à la [176] lumière en quelques centaines de milliers d'années. Dans la seconde hypothèse les dimensions de l'Univers stellaire dont nous faisons partie sont encore décuplées et c'est des millions d'années au moins qu'il faudrait à la lumière pour les parcourir.

Dans le premier cas, l'Univers stellaire tout entier, tel qu'il nous est accessible, est constitué par la Voie Lactée et ses annexes, c'est-à-dire par une concentration locale d'étoiles au delà de laquelle on n'observe rien. L'Univers stellaire est donc pratiquement limité, ou du moins fini.

Dans le cas contraire, la Voie Lactée n'est plus qu'une des myriades de nébuleuses spirales qu'on observe. La nébuleuse spirale (avec ses centaines de millions d'étoiles) joue dans cet Univers agrandi le même rôle que l'étoile dans l'Univers lacté. Le problème se pose comme auparavant, mais sur une plus vaste échelle: de même que la Voie Lactée est formée d'un amas, d'une concentration d'étoiles en nombre fini—cela l'observation le prouve,—de même l'Univers accessible est-il formé d'un amas de nébuleuses spirales en nombre fini?

Sur ce dernier point l'expérience n'a pas encore prononcé. Mais il est probable, à mon sentiment, que lorsque nos instruments seront d'une puissance proportionnée à ce vaste problème, c'est-à-dire bientôt... dans quelques siècles, ils répondront: oui.

S'il en était autrement, si la répartition des nébuleuses spirales restait toujours à peu près la même, à mesure [177] qu'on s'éloigne, le calcul montre que, l'attraction étant en raison inverse du carré des distances, la gravitation croîtrait au delà de toute limite dans cet univers, par exemple dans la région où nous vivons. Or cela n'est pas.

Ceci prouve: soit que, aux très grandes distances, l'attraction de deux masses décroît un peu plus vite que suivant l'inverse du carré des distances (ce qui n'est pas tout à fait impossible), soit que le nombre des systèmes stellaires et des étoiles est fini. Personnellement j'incline vers la seconde hypothèse, mais elle est indémontrable. En ces matières il y a toujours une alternative, toujours un moyen d'échapper suivant la pente de ses préférences, et rien en somme ne permet réellement d'affirmer que le nombre des étoiles est fini.

En partant de la valeur moyenne, telle qu'on l'observe, des mouvements propres des étoiles voisines de nous, Henri Poincaré a calculé que le nombre total des étoiles de la Voie Lactée doit être d'environ 1 milliard. Ce nombre concorde bien avec celui qui résulte expérimentalement des jaugeages astro-photographiques.

Il a montré aussi que les mouvements propres des étoiles devraient être plus forts, s'il y avait beaucoup [178] plus d'étoiles que nous n'en voyons! C'est ainsi que les calculs de Poincaré sont contraires à l'hypothèse d'une extension indéfinie de l'Univers stellaire, puisque le nombre des étoiles «comptées» concorde à peu près avec le nombre qui a été «calculé». Mais, encore un coup, ces calculs ne prouvent plus rien si la loi d'attraction n'est pas tout à fait l'inverse du carré, aux distances énormes.

Pourtant si l'Univers est fini, dans l'espace tel que le conçoit la science classique, la lumière des étoiles et les étoiles isolées elles-mêmes iraient peu à peu se perdre sans retour dans l'infini, et le cosmos s'évanouirait. Notre esprit répugne à cette conséquence et les observations astronomiques ne montrent aucun indice d'une telle dislocation.

En un mot dans l'espace des «absolutistes» l'Univers stellaire ne peut être infini que si la loi du carré des distances n'est pas tout à fait exacte pour des masses très éloignées, et il ne peut être fini que s'il est éphémère dans le temps.

D'ailleurs pour Newton, l'Univers stellaire pourrait être fini dans un Univers infini, puisque l'espace pour lui ne suppose point la matière. Pour Einstein au contraire, l'Univers tout court et l'Univers matériel ou stellaire sont une seule et même chose, puisqu'il n'y a point d'espace sans matière ou énergie.

[179]

Les difficultés et les incertitudes précédentes disparaissent en grande partie lorsqu'on considère l'espace ou plutôt l'espace-temps du point de vue einsteinien de la Relativité généralisée.

Que signifient ces mots: l'Univers est infini? Du point de vue einsteinien, comme du point de vue newtonien, comme du point de vue pragmatiste cela veut dire: Si je marche droit devant moi, toujours et jusqu'à la fin de l'éternité, je ne reviendrai jamais à mon point de départ.

Est-ce possible? Newton dit nécessairement oui, puisque l'espace pour lui s'étend, indéfini, indépendant des corps qui y sont plongés, que le nombre des étoiles soit ou non limité.

Mais Einstein dit: non. Pour le relativiste, l'Univers peut n'être pas infini. Est-il donc borné, limité par je ne sais quelles balustrades? Non. Il n'est pas limité.

Quelque chose peut être illimité sans être infini. Par exemple un homme qui se déplace à la surface de la Terre pourra en faire indéfiniment le tour en tous sens sans être arrêté par une limite. La surface de la Terre ainsi envisagée, comme la surface d'une sphère quelconque est donc à la fois finie et illimitée. Eh bien! il suffit de reporter, dans l'espace à trois dimensions, ce [180] qui se passe dans l'espace à deux dimensions qu'est la surface sphérique, pour comprendre que l'Univers puisse être à la fois fini et illimité.

Nous avons vu que, par suite de la gravitation, l'Univers einsteinien n'est pas euclidien mais incurvé. Il est difficile sinon impossible, nous l'avons déjà dit, de se représenter, de visualiser une incurvation de l'espace. Mais cette difficulté ne doit exister que pour notre imagination limitée par nos habitudes sensibles, non pour notre raison qui va plus loin et plus haut. Car c'est encore une des erreurs les plus fréquentes des hommes de croire que l'imagination a des ailes plus puissantes que la raison. Pour être persuadé du contraire il suffit de comparer ce que les anciens les plus poétiques avaient pu rêver au sujet de la voûte étoilée et ce que la science moderne nous y montre....

Voici alors comment notre problème se pose.

Négligeons, pour l'instant, la répartition un peu irrégulière des étoiles dans notre système stellaire, et supposons-la à peu près homogène. Quelle est la condition pour que cette répartition des étoiles sous l'influence de la gravitation demeure stable? La réponse fournie par le calcul est: pour cela la courbure de l'espace doit être constante et telle que l'espace se ferme sur lui-même à la manière d'une surface sphérique.

Les rayons de lumière des étoiles peuvent faire éternellement, indéfiniment le tour de cet Univers illimité et pourtant fini. Si le cosmos est sphérique de la sorte, on peut même penser que les rayons émanés d'une [181] étoile, du Soleil par exemple, iront converger au point diamétralement opposé de l'Univers après en avoir fait le tour.

On pourrait s'attendre alors à voir, en des points opposés du ciel, des étoiles dont l'une ne serait que l'image, que le fantôme de l'autre, que son «double» au sens où les anciens Égyptiens entendaient ce mot. Au vrai, ce «double», cette étoile-image, nous représenterait, non pas ce qu'est l'étoile génératrice, l'étoile-objet, mais ce qu'elle était à l'époque où elle a émis les rayons qui forment cette image, c'est-à-dire des millions d'années auparavant.

Si d'un point donné du système stellaire, par exemple de notre planète, nous observons en même temps l'étoile-objet et l'étoile-image, la réalité et le mirage, nous les verrons bien différentes l'une de l'autre, puisque l'image nous montrera l'objet tel qu'il était des milliers de siècles auparavant. Il pourra même arriver que l'étoile-image soit plus brillante que l'étoile-objet parce que, dans l'intervalle, celle-ci se sera éteinte, peu à peu refroidie par les siècles.

En fait, il est improbable que nous trouvions souvent de ces astres-fantômes, de ces étoiles-virtuelles, filles lumineuses et irréelles des lourds soleils. La raison en est que les rayons dans leur trajet à travers l'univers [182] seront en général déviés par les étoiles non loin desquelles ils passeront. Leur concentration, leur convergence sera donc rarement parfaite à l'antipode de l'étoile réelle. Et puis ces rayons auront été plus ou moins absorbés par les matières cosmiques rencontrées chemin faisant. Pourtant il n'est point impossible que quelquefois dans l'avenir les astronomes observent ce phénomène. Il n'est point impossible qu'ils l'aient déjà, sans le savoir, observé dans le passé!

Mais ce que les observateurs n'ont pas fait hier, ils le pourront demain grâce aux suggestions de la science nouvelle, et c'est ainsi qu'elle va bouleverser peut-être l'astronomie d'observation et y trouver quelque jour l'éclatante auréole de nouvelles vérifications.

Conséquences étonnantes, follement imprévues, des nouvelles conceptions et qui dépassent par leur poésie fantastique toutes les constructions les plus romanesques de l'extrapolation imaginative.

Le réel ou du moins le possible monte à des hauteurs vertigineuses où jamais n'avaient atteint les ailes dorées de la fantaisie.

J'ai parlé tout à l'heure des millions d'années que la lumière emploie à faire le tour de notre Univers incurvé. C'est qu'en partant de la valeur à peu près connue de la quantité de matière incluse dans la Voie Lactée on peut calculer facilement la courbure du monde et son rayon. On trouve que ce rayon a une valeur au minimum égale à 150 millions d'années de lumière.

[183] Il faut donc au moins 900 millions d'années à la lumière pour faire le tour de l'Univers si celui-ci est limité à la Voie Lactée et à ses annexes. Le chiffre est parfaitement compatible avec ceux que nous ont donnés ci-dessus les observations astronomiques pour la dimension du système galactique, et aussi avec ceux—beaucoup plus grands—que nous avons obtenus en assimilant les nébuleuses spirales à des Voies Lactées.

Ainsi, pour le relativiste, l'Univers peut être illimité sans être infini.

Quant au pragmatiste qui marche droit devant lui—c'est-à-dire qui suit ce qu'il appelle une ligne droite: le trajet de la lumière—il finira forcément par retrouver l'astre d'où il est parti, pourvu qu'il dispose d'un temps suffisant. Il dira donc, si telle est la nature des choses: l'Univers n'est pas infini.

L'infinité ou la finité de l'Univers peut donc en principe être contrôlée par l'expérience, et on pourra vérifier quelque jour si le cosmos dans son ensemble et si l'espace sont newtoniens ou einsteiniens. Malheureusement, c'est une expérience de très longue haleine et qui soulèvera quelques petites difficultés pratiques.

On peut donc, sans trop se compromettre jusqu'à nouvel ordre, ne pas se croire obligé de choisir entre les deux conceptions et laisser planer le bénéfice du doute sur celle des deux qui est fausse....

[184]

Il y a d'ailleurs peut-être encore une troisième issue sinon pour le pragmatiste, du moins pour le philosophe, j'entends par là le physicien, me souvenant que les Anglais appellent la physique Natural Philosophy.

Voici: si tout ce que nous connaissons d'astres se rattache à notre Voie Lactée, d'autres Univers très éloignés peuvent nous être inaccessibles parce qu'ils sont optiquement isolés du nôtre, peut-être par les phénomènes d'absorption cosmique de la lumière dont nous avons parlé déjà.

Mais ceci pourrait être aussi causé par autre chose qui choquera peut-être quelques relativistes mais semblera possible aux newtoniens. L'éther, ce milieu qui transmet les vibrations lumineuses et dont Einstein lui-même a fini par réadmettre l'existence tout en lui refusant ses propriétés cinématiques habituelles; l'éther, dis-je, et la matière, semblent de plus en plus n'être que des modalités l'un de l'autre. Nous l'avons expliqué dans un chapitre précédent, d'après les découvertes physiques les plus récentes. Rien ne prouve donc que ces deux formes de la substance ne soient pas toujours associées l'une à l'autre.

N'ai-je pas alors le droit de penser que peut-être notre Univers visible tout entier, concentration locale de matière, n'est qu'une bulle d'éther isolée? Si l'espace absolu existe (ce qui ne veut pas dire qu'il nous soit [185] sensible, accessible), il est indépendant non seulement de la matière, mais de l'éther. Et alors, autour de notre Univers, s'étendent des espaces vides d'éther. D'autres Univers, peut-être, palpitent au delà, et ces mondes sont à jamais pour nous comme s'ils n'étaient pas.

Rien de sensible, rien de connaissable ne peut nous en parvenir; rien ne peut franchir les abîmes noirs et muets qui entourent notre île stellaire.

Nos regards sont à jamais prisonniers dans cette monade géante... et déjà trop petite.

«Il y a donc des choses qu'on ne saura jamais et qui, pourtant, existent peut-être?» vont s'écrier les naïfs étonnés. Plaisante prétention de vouloir tout contenir dans quelques centimètres cubes de substance grise....

Le temps et l'espace, ces deux pôles autour desquels tournait la sphère des données sensibles, et qu'on croyait inébranlables se sont vus déposséder de leur puissante fixité. A leur place Einstein fait surgir ce continuum où baignent les êtres et les phénomènes: l'espace-temps à quatre dimensions et où le temps et l'espace sont liés à un joug commun.

[187] Mais ce continuum lui-même n'est plus qu'une forme flasque, sans rigidité et qui docilement s'applique à tout. Plus rien de fixe, puisque aucun repère défini n'existe, où nous puissions encadrer les phénomènes; puisque au bord de l'océan où flottent les choses, il ne reste plus aucun de ces solides anneaux où les marins naguère amarraient les vaisseaux.

Jusqu'ici la théorie de la relativité mérite bien son nom. Mais voici que malgré elle, encore que par elle et en dépit de son nom même, surgit quelque chose qui dans le monde extérieur semble avoir une existence indépendante et déterminée, une objectivité, une réalité absolue. C'est l'Intervalle des événements qui, lui, à travers toutes les fluctuations des choses, quelle que soit la diversité infinie des points de vue, la mobilité des repères, demeure constant, invariable.

De cette donnée, qui, philosophiquement parlant, participe étrangement des qualités intrinsèques tant reprochées au vieil espace absolu, au vieux temps absolu, dérive en réalité toute la partie constructive de la Relativité, toute celle qui a conduit aux splendides vérifications que nous avons dites.

Ainsi la théorie de la Relativité, dans ce qui en fait un monument scientifique utile, un outil constructif, un instrument de découverte, semble renier son nom et sa source même. Elle est une théorie d'un nouvel absolu: l'Intervalle représenté par les géodésiques de l'Univers quadridimensionnel. Elle est une nouvelle théorie absolue. Tant il est vrai que, même dans la [188] science, on ne construit rien sur la négation pure.

Pour créer il faut affirmer.

La théorie de la Relativité a obtenu des victoires éclatantes que la sanction impérieuse des faits a couronnées. Nous en avons donné, dans les chapitres précédents, les exemples les plus étonnants. Mais dire de cette théorie qu'elle est vraie parce qu'elle a prédit des phénomènes vérifiés ensuite, ce serait la juger d'un point de vue trop étroitement pragmatiste. Ce serait aussi—et il y a là un danger—barrer la route à des élans de la pensée vers d'autres chemins où il y aura encore des fleurs à cueillir. Gardons-nous-en bien.

Il importe donc en dépit et à cause même de ses succès, de diriger sur les bases de la doctrine nouvelle le faisceau lumineux de la critique. César montant au Capitole devait entendre auprès de son char les soldats plaisanter ses travers et rabattre sa superbe. La théorie de la Relativité, si magnifiquement qu'elle avance sur la voie triomphale, doit elle aussi connaître qu'elle a des limites et peut-être des faiblesses.

Avant de la fouiller pourtant, avant d'y projeter une lumière crue, une remarque s'impose.

Quelles que soient les incertitudes des théories physiques, quelle que soit l'imperfection éternelle et fatale de la science, une chose doit être ici affirmée: Les vérités [189] scientifiques sont les mieux fondées, les plus certaines, les moins douteuses des vérités que nous puissions connaître touchant le monde extérieur. Si la science ne peut nous dévoiler tout à fait la nature des choses, il n'est rien qui puisse nous la faire connaître autant qu'elle. Les vérités du sentiment, de la foi, de l'intuition sont irréductibles à celles de la science tant qu'elles restent des vérités du monde intérieur; elles sont sur un autre plan.

Mais si elles prétendaient se montrer adéquates au monde extérieur—ce qui serait leur seule cause de faiblesse—elles se subordonnent dès cet instant à la réalité sensible, à la recherche scientifique de la vérité.

C'est donc un non-sens de vouloir opposer la prétendue «faillite de la science» à la certitude que d'autres disciplines nous apportent touchant le monde extérieur. La faillite de l'une entraîne celle des autres. Tant qu'il ne s'agit plus de l'oasis intime où fleurissent les sereines réalités du sentiment, mais du désert aride et mal exploré du monde extérieur, les données scientifiques sont la base de toutes les autres. Ébranler celles-là, c'est ébranler celles-ci. Un coup de bélier dans un rez-de-chaussée, s'il le fait écrouler, démolit sûrement aussi les étages supérieurs.

Au vrai, il semble que rien ne manifeste ici-bas la présence mystique du divin autant que cette harmonie éternelle et inflexible qui lie les phénomènes et qu'expriment les lois scientifiques. La science qui nous montre le vaste univers ordonné, cohérent, harmonieux, [190] mystérieusement uni, organisé comme une vaste et muette symphonie, dominé par la loi et non par le caprice, par des règles inéluctables et non par des volontés particulières, la science n'est-elle pas, après tout, une Révélation?

Là doit être, là sera la conciliation nécessaire entre les esprits dociles à la réalité sensible et ceux qu'obsède le mystère métaphysique.

Proclamer la faillite de la science, si cela veut dire autre chose que proclamer la faiblesse humaine, dont nul ne doute hélas! c'est en réalité dénigrer cette part du divin qui est accessible à nos sens, celle que la science nous dévoile.

En somme, toute la synthèse einsteinienne découle du résultat de l'expérience de Michelson, ou du moins d'une interprétation particulière de ce résultat.

Le phénomène de l'aberration des étoiles prouve que le milieu qui transmet leur lumière jusqu'à notre œil ne participe pas à la translation de la Terre autour du Soleil. Ce milieu les physiciens l'appellent l'éther. Lord Kelvin qui a mérité l'honneur de reposer à Westminster sous la dalle contiguë à celle où gît Newton, considérait avec raison l'existence de l'éther interstellaire comme aussi bien prouvée que celle de l'air que nous respirons; car sans ce milieu la chaleur solaire, mère et nourrice de toute vie terrestre, ne parviendrait pas jusqu'à nous.

[191] Dans la théorie de la relativité restreinte, Einstein, nous l'avons vu, interprète les phénomènes sans faire intervenir l'éther, ou du moins sans faire intervenir les propriétés cinématiques habituellement attribuées à cette substance. Autrement dit la relativité restreinte n'affirme ni ne nie l'éther classique; elle l'ignore.

Mais cette indifférence à l'égard de l'éther, ce dédain disparaît dans la théorie de la Relativité généralisée. Nous avons vu dans un chapitre précédent que les trajectoires des corps gravitants et de la lumière procèdent directement, d'après cette théorie, d'une courbure particulière et du caractère non euclidien du milieu qui, dans le vide, avoisine les corps massifs, c'est-à-dire de l'éther. Celui-ci, bien que ses propriétés cinématiques ne soient pas pour Einstein ce qu'elles sont pour les classiques, devient le substratum de tous les événements de l'Univers. Il reprend son importance, sa réalité objective. Il est le milieu continu où évoluent les faits spatio-temporels.

Donc sous sa forme générale, et en dépit de l'attitude cinématique nouvelle qu'elle lui attribue, la théorie générale d'Einstein admet l'existence objective de l'éther.

L'aberration des étoiles montre ce milieu immobile par rapport à la translation de la Terre sur son orbite.

Le résultat négatif de l'expérience de Michelson tend au contraire à prouver qu'il participe à ce mouvement de la Terre. L'hypothèse de Fitzgerald-Lorentz concilie cette antinomie en admettant que l'éther ne participe réellement pas à la translation terrestre, mais que tous [192] les corps qui s'y déplacent subissent dans le sens de ce déplacement une contraction. Celle-ci croît avec leur vitesse dans l'éther, ce qui explique le résultat négatif de Michelson.

L'explication de Lorentz a paru inadmissible à Einstein, à cause de quelques invraisemblances que nous avons signalées, et surtout parce qu'elle suppose l'existence dans l'Univers d'un système de références privilégiées qui ressuscite l'espace absolu de Newton. Einstein en vertu du principe que tous les points de vue sont également relatifs, n'admet pas qu'il y ait dans l'Univers des observateurs privilégiés—ceux qui sont immobiles dans l'éther—qui verraient les choses telles qu'elles sont tandis que ces choses seraient déformées pour tout autre observateur.

Et alors, tout en conservant la contraction de Lorentz et les formules qui l'expriment, Einstein affirme que cette contraction existe, mais n'est qu'une apparence, une sorte d'illusion d'optique provenant de ce que la lumière qui nous définit les objets ne se propage pas instantanément, mais avec une vitesse finie. Cette propagation de la lumière se fait suivant des lois telles que précisément l'espace et le temps apparent soient déformés conformément aux formules de Lorentz. Telle est la base de la relativité spéciale d'Einstein.

Ainsi les deux premières explications possibles du résultat négatif de l'expérience de Michelson sont:

1^o Il y a une contraction des objets mobiles dans l'éther immobile, substratum fixe des phénomènes. Cette [193] contraction est réelle, croît avec la vitesse du mobile par rapport à l'éther. C'est l'explication de Lorentz.

2^o Il y a une contraction des objets mobiles par rapport à un observateur quelconque. Cette contraction n'est qu'une apparence due aux lois de la propagation de la lumière. Elle croît avec la vitesse du mobile par rapport à l'observateur. C'est l'explication d'Einstein.

Mais il y a encore—pour le moins—une troisième explication possible. Elle introduit des hypothèses nouvelles et même insolites, mais nullement absurdes. D'ailleurs c'est surtout en physique que le vrai peut quelquefois n'être pas vraisemblable. Elle montrera, que même en dehors de celle de Lorentz, on peut rendre compte du résultat de Michelson autrement que par l'interprétation einsteinienne.

Voici cette troisième hypothèse explicative:

Chaque corps matériel entraîne avec lui, comme une sorte d'atmosphère, l'éther qui lui est lié. Il existe en outre dans le vide interastral un éther immobile, insensible au mouvement des corps matériels qui s'y meuvent, et que, pour le distinguer de l'éther lié aux corps, nous appellerons le suréther. Ce suréther occupe tout le vide interstellaire et se superpose près des astres à l'éther qu'ils entraînent. L'éther et le suréther se transpénètrent de même qu'ils transpénètrent la matière, et les vibrations [194] qu'ils transmettent s'y propagent indépendamment. Quand un corps matériel émet des trains d'ondes dans l'éther qui l'entoure, celles-ci sont animées par rapport à lui de la vitesse constante de la lumière. Mais lorsqu'elles ont traversé la couche relativement mince d'éther liée à ce corps matériel, et qui se fond graduellement dans le suréther, c'est dans celui-ci que se fait leur propagation et c'est par rapport à lui qu'elles prennent progressivement leur vitesse.

C'est ainsi qu'un bateau traversant le lac de Genève avec une certaine vitesse possède, vers le milieu du lac, cette vitesse par rapport à l'étroit courant qu'y fait le Rhône, puis la reprend par rapport au lac immobile.

Ainsi, bien qu'émanées d'astres qui s'éloignent ou s'approchent de nous, les rayons lumineux des étoiles posséderont la même vitesse lorsqu'ils nous parviendront, et qui sera la vitesse commune que leur impose le suréther. Ainsi, d'autre part, les rayons des étoiles arrivant à nos lunettes seront propagés jusqu'à nous par le suréther et sans que la très mince couche d'éther mobile avec la Terre ait pu troubler cette propagation.

Dans ces hypothèses tous les faits s'expliquent et se concilient: 1^o l'aberration des étoiles, parce que les rayons qui nous en arrivent nous sont transmis sans altération par le suréther; 2^o le résultat négatif de l'expérience de Michelson, parce que la lumière que nous produisons au laboratoire se propage dans l'éther entraîné par la Terre et où elle est née; 3^o le fait qu'en [195] dépit du rapprochement ou de l'éloignement des étoiles, leurs rayons nous arrivent avec la vitesse commune qu'ils ont acquise dans le suréther, peu après leur émission.

Cette explication, si étrange qu'elle puisse paraître, n'est pas absurde et ne soulève aucune difficulté qu'on ne puisse surmonter. Elle prouve que si le résultat de Michelson constitue une sorte de cul-de-sac, il est pour en sortir d'autres issues que la théorie d'Einstein.

En résumé, pour échapper aux difficultés, aux apparentes contradictions manifestées par l'expérience, à l'antinomie qui existe entre l'aberration et le résultat de Michelson, trois voies nous sont offertes, et qui se ramènent à cette alternative:

1^o La contraction des corps par la vitesse est réelle (Lorentz).

2^o La contraction des corps par la vitesse n'est qu'une apparence due aux lois de propagation de la lumière (Einstein).

3^o La contraction des corps par la vitesse n'est ni une réalité ni une apparence; elle n'existe pas (hypothèse du suréther conjugué à l'éther).

Cela prouve que l'explication einsteinienne des phénomènes n'est nullement imposée par les faits, ou du moins n'est pas imposée par eux impérativement et à l'exclusion de toute autre.

[196]

Est-elle du moins imposée par la raison, par les principes, par le caractère d'évidence de ses prémisses rationnelles, parce qu'elle ne choque pas, à l'égal des autres, le bon sens et nos habitudes mentales?

On pourrait le croire d'abord, lorsqu'on la compare à la doctrine de Lorentz,—et pour ne pas surcharger cette discussion, je laisserai provisoirement de côté la troisième théorie explicative qui a été esquissée, celle du suréther.

Ce qui a paru choquant dans l'hypothèse de la contraction réelle de Lorentz c'est en premier lieu que cette contraction ne dépend que de la vitesse des objets, nullement de leur nature; c'est qu'elle est la même pour tous quelle que soit leur substance, leur composition chimique, leur état physique.

A la réflexion cette chose étrange paraît moins inadmissible. Ne savons-nous pas en effet que les atomes sont tous formés des mêmes électrons dont l'arrangement et le nombre atomique diffèrent seuls et seuls différencient les corps.

Si alors les électrons communs à toute matière subissent ensemble, de même que leurs distances relatives, une contraction due à la vitesse, il est en somme assez naturel de penser que le résultat puisse être identique pour tous les objets. Quand la chaleur dilate une grille de fer de longueur donnée, la quantité dont une température de cent degrés surélève et élargit cette grille sera [197] la même, que celle-ci compte dix barreaux ou cent barreaux d'acier au mètre courant, pourvu qu'ils soient identiques.

Ce n'est donc pas là en définitive que réside l'invraisemblance qui a fait rejeter par les relativistes la théorie de Lorentz.

C'est dans les principes mêmes de cette théorie, c'est parce qu'elle admet dans la nature un système de référence privilégié, l'éther immobile par rapport à quoi les corps se déplacent.

Examinons cela d'un peu plus près.

On a dit que l'éther immobile de Lorentz est en somme une résurrection de l'espace absolu de Newton tant attaqué par les relativistes. Rien n'est moins sûr. Si, comme nous l'avons supposé dans le chapitre précédent, notre Univers stellaire n'est qu'une gigantesque bulle d'éther divaguant dans un espace vide d'éther, parmi d'autres bulles d'éther à jamais inconnaissables à l'homme, il est évident que la gouttelette éthérée qui constitue notre Univers peut très bien être en mouvement dans l'espace qui l'entoure et qui serait le véritable espace absolu.

De ce point de vue, l'éther lorentzien ne peut donc être assimilé à l'espace absolu. Faire cette assimilation revient à dire que l'espace dénommé absolu par Newton ne mérite peut-être pas ce nom. Si l'espace newtonien n'est que le continu physique où se déroulent les événements de notre Univers particulier, il n'est alors rien moins qu'absolument immobile.

[198] Toute la querelle faite à Newton revient en ce cas à lui reprocher une impropriété d'expression, et d'avoir appelé absolu ce qui n'est que privilégié pour un Univers donné.

Ce serait une querelle grammaticale, et Vaugelas n'a jamais suffi à bouleverser la Science.

Mais les relativistes, ou du moins ces relativistes impénitents que sont les einsteiniens ne se contenteront pas de cela. Il ne leur suffit point que l'espace newtonien avec tous ses privilèges ne soit peut-être pas l'espace absolu.

Notre conception de l'Univers, île mouvante d'éther, concilierait très bien la prééminence de l'espace newtonien et l'agnosticisme qui nous dénie toute emprise sur l'absolu. Cela encore un coup ne suffit pas aux einsteiniens. Ce qu'ils entendent faire, c'est dépouiller résolument l'espace newtonien sur lequel a été construit la mécanique classique, de tous ses privilèges. C'est faire rentrer cet espace dans le rang, c'est le réduire à être l'analogue de tous les autres espaces qu'on peut imaginer et qui se meuvent arbitrairement par rapport à lui: rien de plus.

Du point de vue agnostique, du point de vue sceptique et douteur, cette attitude est forte et belle. Mais au cours de ce volume nous avons assez admiré la [199] puissante synthèse théorique d'Einstein et les surprenantes vérifications à quoi elle a conduit, pour avoir le droit de faire maintenant nos réserves. On peut mettre en doute même les dénégations des douteurs, car elles aussi, en fin de compte sont des affirmations.

Nous croyons qu'en face de l'attitude philosophique des einsteiniens, en face de ce que j'appellerais volontiers leur relativisme absolu, il est permis de s'insurger un peu et de dire ceci:

Oui, tout est possible, ou du moins beaucoup de choses sont possibles mais toutes ne sont pas. Oui, si je pénètre dans un appartement inconnu, la pendule du salon peut être ronde, carrée ou octogone. Mais lorsque franchissant la porte j'ai vu que cette pendule est carrée, j'ai le droit de dire: elle est carrée; elle a le privilège d'être carrée, c'est un fait qu'elle n'est ni ronde, ni octogone.

De même dans la nature. Le continu physique qui, comme un vase, épouse les phénomènes de l'Univers, pourrait avoir par rapport à moi—et tant que je ne l'ai pas observé—des mouvements ou des formes quelconques. Mais en fait, il est ce qu'il est, et il ne peut être en même temps des choses différentes. L'horloge du salon ne peut être à la fois toute en or et toute en argent.

On peut donc concevoir, parmi les possibilités que nous imaginons dans le monde extérieur, une possibilité privilégiée: celle qui est effectivement réalisée, celle qui existe.

Le relativisme total des einsteiniens revient à affirmer l'Univers tellement extérieur à nous que nous [200] n'avons aucun moyen d'y distinguer le réel du possible, en ce qui concerne l'espace et le temps. Les newtoniens au contraire affirment que l'espace réel, le temps réel se manifestent à nous par des signes particuliers. Nous analyserons plus loin ces signes.

En somme les relativistes purs ont cherché à échapper à la nécessité de supposer une réalité inaccessible.

C'est un point de vue à la fois beaucoup plus modeste et beaucoup plus outrecuidant que celui des newtoniens, des «absolutistes».

Plus modeste, parce que selon l'einsteinien nous ne pouvons pas connaître certaines choses que l'absolutiste pense au contraire pouvoir approcher: le temps et l'espace réels. Plus outrecuidant, parce que le relativiste affirme qu'il n'y a pas de réalité autre que celle qui est accessible à l'observation. Pour lui inconnaissable et inexistant sont presque synonymes. C'est pourquoi Henri Poincaré qui fut, avant Einstein, le plus profond des relativistes répétait sans cesse que les questions concernant l'espace et le temps absolus n'ont «aucun sens».

En définitive les einsteiniens ont fait leur devise du mot d'Auguste Comte: Tout est relatif et cela seul est absolu.

En face, Newton dont Henri Poincaré se refusait énergiquement à admettre les prémisses spatio-temporelles, et avec lui la science classique, ont une attitude que Newton a admirablement définie lui-même lorsqu'il écrivait: «Je ne suis qu'un enfant qui joue sur le rivage, m'amusant à trouver de temps en temps un caillou [201] mieux poli ou un coquillage plus beau que d'ordinaire, pendant que le grand océan de la vérité reste toujours inexploré devant moi.» Newton affirme que cet océan est inexploré, seulement il affirme qu'il existe, et de la forme des coquillages trouvés, il déduit certaines des qualités de cet océan, et notamment celles qu'il appelle le temps et l'espace absolus.

Einsteiniens et newtoniens sont d'accord pour penser que le monde extérieur n'est pas aujourd'hui totalement réductible à la science. Mais leur agnosticisme a des limites différentes. Les newtoniens croient que, si extérieur que nous soit le monde, il ne l'est pas au point que le temps réel et l'espace réel nous soient inaccessibles. Les einsteiniens sont d'un autre avis. Ce qui les sépare c'est seulement une question de degré dans le scepticisme.

Toute la controverse se ramène à une contestation de frontières entre deux agnosticismes.

Ces signes, ces critères sont implicitement à la base du développement de la science classique. Pourtant ils étaient un peu restés dans l'ombre des discussions provoquées par le système d'Einstein.

Délaissant un moment d'autres soins peut-être moins nobles, M. Paul Painlevé vient, devant l'Académie des Sciences, d'attirer avec éclat l'attention sur les [203] raisons anciennes mais toujours vigoureuses qui ont communiqué leur force à la conception newtonienne du monde.

L'espace absolu, le temps absolu de Newton et de Galilée, appelons-les désormais l'espace privilégié, le temps privilégié, pour ne plus prêter le flanc aux objections métaphysiques assez justifiées en somme, que le qualificatif absolu pouvait soulever.

Pourquoi la science classique, la mécanique de Galilée et de Newton sont-elles fondées sur l'espace privilégié, le temps privilégié? Pourquoi rapportent-elles tous les phénomènes à ces repères uniques qu'elles considèrent comme adéquats à la réalité? C'est à cause du principe de causalité.

Ce principe peut s'énoncer ainsi: des causes identiques produisent des effets identiques. Cela veut dire que les conditions initiales d'un phénomène déterminent ses modalités ultérieures. C'est en somme l'affirmation du déterminisme des phénomènes, sans lequel la science est impossible.

Assurément on peut chicaner là-dessus. Des conditions parfaitement identiques à des conditions initiales données ne peuvent jamais être reproduites ou retrouvées, en un autre temps ou en un autre lieu. Il y a toujours quelque circonstance qui ne sera plus la même, par exemple le fait que, entre les deux expériences, la Nébuleuse d'Andromède se sera rapprochée de nous de quelques milliers de kilomètres. Et nous sommes sans action sur la Nébuleuse d'Andromède.

[204] Heureusement, et cela sauve tout, les corps éloignés n'ont qu'une action négligeable, semble-t-il, sur nos expériences, et c'est pourquoi nous pouvons répéter celles-ci.

Par exemple, si nous mettons aujourd'hui un gramme d'acide sulfurique fumant dans dix grammes de solution de soude au dixième, ces corps produiront dans le même temps, la même quantité du même sulfate de soude qu'ils eussent fait l'an passé, dans les mêmes conditions de température et de pression, et bien que dans l'intervalle le maréchal Foch ait débarqué aux États-Unis.

Cela fait que le principe de causalité (mêmes causes, mêmes effets) est toujours vérifié et ne pourra jamais être pris en défaut. Ce principe est donc une vérité d'expérience, mais en outre il s'impose à notre entendement avec une puissance irrésistible.

Il s'impose même aux animaux. Le proverbe «Chat échaudé craint même l'eau froide» le prouve.... Il prouve aussi qu'on peut interpréter abusivement ce principe.... En tout cas, non seulement la science, mais la vie tout entière des hommes et des bêtes sont fondées sur lui.

La conséquence de ce principe, c'est que si les conditions initiales d'un mouvement présentent une symétrie, celle-ci se retrouvera dans le mouvement. M. Paul Painlevé vient d'y insister avec force au cours de la discussion récente du Relativisme à l'Académie des Sciences. De cette remarque découle notamment le [205] principe de l'inertie: un corps abandonné librement loin de toute masse matérielle, restera immobile ou décrira une ligne droite, par raison de symétrie.

Il décrira effectivement une droite pour un certain observateur (ou pour des observateurs animés de vitesses uniformes par rapport au premier). Les newtoniens disent que l'espace de ces observateurs est privilégié.

Au contraire, pour un autre observateur animé par rapport à ceux-là d'un mouvement accéléré, la trajectoire du mobile est une parabole et n'est plus symétrique. Donc l'espace de ce nouvel observateur n'est pas l'espace privilégié.

Il me semble qu'à cela les relativistes peuvent répondre: Vous n'avez pas le droit de définir les conditions initiales pour un observateur donné, puis le mouvement subséquent pour un autre animé d'une vitesse accélérée. Si vous définissez aussi vos conditions initiales par rapport à celui-ci, le mobile à l'instant qu'on l'abandonne n'est pas libre pour cet observateur, mais tombe dans un champ de gravitation. Rien d'étonnant alors à ce que le mouvement produit lui semble accéléré et dissymétrique. Le principe de causalité n'est en défaut ni pour l'un ni pour l'autre des observateurs.

On peut aussi définir autrement le système privilégié en disant: c'est celui par rapport auquel la lumière se propage en ligne droite dans un milieu isotrope. Mais en ce cas, pour un observateur fixé à la Terre qui [206] tourne, les rayons des étoiles se déplacent en spirale, et les newtoniens en déduiraient que la Terre tourne par rapport à leur espace privilégié. Les einsteiniens répliqueront que l'espace où circulent ces rayons n'est pas isotrope et qu'ils y sont déviés de la ligne droite par le champ de gravitation tournant qui cause la force centrifuge de la rotation terrestre. Il y aura toujours pour eux une échappatoire qui laissera intact le principe de causalité.

Il semble donc difficile de démontrer sans réplique l'existence du système privilégié en partant du principe de causalité et chacun reste sur ses positions.

En revanche il y a une force d'évidence, une pénétration aiguë et convaincante dans la seconde partie des critiques élevées par M. Painlevé contre les principes de la doctrine einsteinienne.

Résumons l'argumentation du célèbre géomètre. Vous déniez, dit-il aux einsteiniens, tout privilège à un système de référence quelconque. Mais lorsque, de vos équations générales, vous voulez déduire par le calcul la loi de la gravitation, vous ne pouvez le faire et vous ne le faites réellement, qu'en introduisant des hypothèses newtoniennes à peine déguisées et des axes de référence privilégiés. Vous n'arrivez au résultat de votre calcul qu'en séparant nettement le temps de [207] l'espace comme Newton, et en rapportant vos mobiles gravitants à des axes privilégiés purement newtoniens, et pour lesquels certaines conditions de symétrie sont réalisées.

Toute cette fine et profonde critique de M. Painlevé est à rapprocher de celle de Wiechert qui a déniché diverses autres hypothèses introduites, chemin faisant, dans les calculs d'Einstein.

En définitive, celui-ci paraît ne s'être pas complètement dégagé des prémisses newtoniennes qu'il répudie. Il ne les dédaigne pas autant qu'on pourrait croire et ne craint pas, à l'occasion, de les appeler à son secours, quand il s'agit de faire aboutir le calcul.

C'est proprement un peu adorer ce qu'on a brûlé.

Pour se tirer d'affaire, les einsteiniens répondront sans doute que s'ils introduisent des axes newtoniens, au cours de leurs développements, c'est pour rendre le résultat du calcul comparable à celui des mesures expérimentales. Les axes ainsi introduits dans les équations ont pour les relativistes cet unique privilège d'être ceux auxquels les expérimentateurs rapportent leurs mesures. Mais on conviendra que ce n'est pas là un mince privilège.

Ce n'est pas tout. Le principe de relativité généralisée dit en somme ceci: tous les repères, tous les systèmes de référence sont équivalents pour exprimer [208] les lois de la nature et ces lois sont invariantes à quelque système de référence qu'on les rapporte. Cela veut dire en somme: il y a entre les objets du monde extérieur des relations qui sont indépendantes de celui qui les regarde, et notamment de sa vitesse. Ainsi un triangle étant tracé sur un papier, il y a dans ce triangle quelque chose qui le caractérise et qui est identique, que le regardant passe très vite ou très lentement ou avec des vitesses quelconques et en sens quelconque devant le papier.

M. Painlevé remarque avec quelque raison que, sous cette forme, le principe est une sorte de truisme. Le mot est dur. Il exprime pourtant un fait certain. Les rapports réels des objets extérieurs ne peuvent être altérés par le point de vue de l'observateur.

Einstein répondra que c'est déjà quelque chose de fournir un crible au travers duquel doivent passer, un critère auquel doivent satisfaire pour être reconnues exactes, les lois et formules qui servent à représenter les phénomènes empiriquement observés. Il est vrai. La loi de Newton sous sa forme classique ne satisfaisait pas à ce critère. Cela prouve qu'il n'était pas si évident que cela. Il arrive qu'une vérité méconnue hier devienne aujourd'hui un truisme. Tant mieux.

En exprimant une des conditions auxquelles doivent satisfaire les lois naturelles, la théorie de la relativité acquiert pour le moins ce que dans le jargon philosophique on appelle une valeur «heuristique.»

Il n'en est pas moins certain, comme M. Painlevé le [209] montre avec une vigueur et une clarté parfaites, que le principe de la relativité généralisée ainsi considéré, ne saurait suffire à fournir des lois précises. Il serait parfaitement conciliable avec une loi de gravitation où l'attraction serait en raison inverse, non pas du carré, mais de la dix-septième, de la centième puissance, d'une puissance quelconque de la distance.

Pour extraire du principe de la relativité généralisée la loi exacte de l'attraction, il faut y surajouter l'interprétation einsteinienne du résultat de Michelson à savoir: que par rapport à un observateur quelconque la lumière se propage localement avec la même vitesse en tous sens. Il faut surajouter encore diverses hypothèses que M. Painlevé considère comme newtoniennes.

A son exposé critique de la relativité présenté avec éclat devant l'Académie des Sciences, M. Paul Painlevé a ajouté une contribution mathématique précieuse dont le principal résultat est le suivant: on peut trouver d'autres lois de la gravitation que celle indiquée par Einstein et qui toutes correspondent aux conditions einsteiniennes.

Le savant géomètre français en a indiqué plusieurs, une en particulier dont la formule nettement différente de celle d'Einstein, rend compte comme celle-ci et avec précision du mouvement des planètes, du déplacement du périhélie de Mercure, et de la déviation des rayons lumineux près du Soleil.

Cette formule nouvelle correspond à un espace qui est indépendant du temps, et elle n'entraîne pas la conséquence [210] qui dérive de la formule d'Einstein au sujet du déplacement vers le rouge de toutes les raies spectrales du Soleil.

La vérification ou la non vérification de cette conséquence de l'équation d'Einstein dont nous avons dans un chapitre précédent indiqué les difficultés—peut-être insurmontables—en acquiert une importance nouvelle.

Chose remarquable, plusieurs des formules de gravitation données par M. Painlevé conduisent, contrairement à celle d'Einstein, à la conclusion que l'espace reste euclidien lorsqu'on s'approche du Soleil, en ce sens que les mètres ne doivent pas nécessairement se raccourcir.

Tout cela brille à l'horizon de l'astronomie comme l'aurore d'une époque nouvelle où des observations d'un raffinement insoupçonné fourniront les critères délicats, capables d'imposer une forme plus précise, plus exempte d'ambiguïté à la loi de la gravitation. Il y a encore de beaux jours... ou plutôt de belles nuits pour les astronomes.

Pour ce qui est des principes la controverse continuera. Elle doit en définitive aboutir à un dialogue dans le genre de celui-ci.

Le newtonien: Admettez-vous qu'en un point de l'Univers très éloigné de toutes masses matérielles, un [211] mobile abandonné à lui-même doit décrire une ligne droite? En ce cas vous reconnaissez l'existence d'observateurs privilégiés, ceux pour lesquels cette ligne est droite. Pour un autre observateur il arrive que cette ligne est une parabole. Donc son point de vue est faux.

Le relativiste: Oui, je l'admets, mais en fait, il n'existe aucun point de l'Univers où l'action des masses matérielles éloignées soit nulle. Par conséquent votre mobile abandonné librement n'est qu'une abstraction, et je ne peux fonder la science sur une abstraction invérifiable. Tout l'effort du relativiste est de débarrasser la science de ce qui n'a pas un sens expérimental.

Quant à l'observateur qui voit le mobile supposé décrire une ligne parabolique, il interprétera son observation en disant que le mobile est dans un champ de gravitation.

Le newtonien: Vous êtes donc obligé d'admettre que très loin de toute matière, très loin de tous les astres, il peut exister ce que vous appelez un champ de gravitation, que celui-ci varie selon la vitesse de l'observateur, et qu'il pourra être très intense en dépit de la distance des astres et même croître parfois avec cette distance. Ce sont des hypothèses étranges et absurdes.

Le relativiste: Elles sont étranges mais je vous défie de démontrer qu'elles sont absurdes. Elles le sont moins que de localiser et mettre en mouvement un point isolé et indépendant de toute masse matérielle.

Le newtonien: Quant à moi j'imagine très bien un point matériel unique dans l'Univers, et qui y posséderait [212] une certaine position et une certaine vitesse.

Le relativiste: Pour moi, au contraire, si un tel point matériel existait, il serait absurde et impossible de parler de sa position et de son mouvement. Ce point n'aurait ni position, ni mouvement, ni immobilité. Ces choses ne peuvent exister que par rapport à d'autres points matériels.

Le newtonien: Tel n'est pas mon avis.

Le spectateur impartial: Pour savoir qui a raison il faudrait faire une expérience sur un point matériel soustrait à l'action du reste de l'Univers. Pouvez-vous, messieurs, faire cette expérience?

Le newtonien et le relativiste (ensemble): Non, hélas!

Le métaphysicien (survenant comme le troisième larron de la fable): Pour lors, messieurs, je vous engage à retourner à vos télescopes, à vos laboratoires et à vos tables de logarithmes. Le reste me regarde.

Le newtonien et le relativiste (ensemble): En ce cas nous sommes bien sûrs de ne jamais rien apprendre de plus là-dessus que ce que nous savons et croyons déjà.

Au demeurant, on ne saurait s'exagérer l'importance des clartés nouvelles projetées dans la question de la relativité par l'intervention de M. Paul Painlevé à l'Académie des Sciences. Le retentissement en sera immense et durable.

[213] L'admirable synthèse einsteinienne en sera-t-elle abattue? S'ébranlera-t-elle jusqu'à crouler sous les controverses, les doutes, les incertitudes dont nous venons de donner un bref aperçu? Je ne le crois pas.

Quand Christophe Colomb a découvert l'Amérique, on eut beau jeu de lui dire que ses prémisses étaient fausses et que s'il n'avait cru partir pour les Indes, il n'eût jamais atteint un continent nouveau. Il aurait pu répondre à la manière de Galilée: «Et pourtant je l'ai découvert.»

Celle qui donne de beaux résultats est toujours une bonne méthode.

Dès qu'il s'agit de plonger au fond de l'inconnu pour trouver du nouveau, dès qu'il s'agit de savoir plus et mieux, la fin justifie les moyens.

En montrant du doigt l'optique, la mécanique, la gravitation liées solidement en une neuve gerbe, la déviation de la lumière par la gravité qu'il a annoncée contre toute attente, les anomalies de Mercure qu'il a le premier expliquées, la loi de Newton qu'il a embellie et précisée, Einstein aurait le droit de s'écrier avec quelque orgueil: «Voilà ce que j'ai fait.»

Les voies par lesquelles il a obtenu tous ces résultats admirables ne sont pas exemptes, dit-on, de détours assez fâcheux et de fondrières. C'est donc que plusieurs chemins, et même imparfaits, peuvent mener à Rome et à la vérité. L'essentiel est d'y parvenir. Et ici la vérité, ce sont des faits anciens rapprochés par une harmonie supérieure, ce sont des faits nouveaux annoncés en [214] des équations prophétiques et vérifiés de la manière la plus surprenante.

Si la discussion des principes, si la théorie qui n'est que la servante du savoir, hoche un peu devant l'œuvre d'Einstein ses épaules serviles et infidèles, du moins l'expérience, source unique de toute vérité, lui a donné raison.

On découvre aujourd'hui des formules brillantes que n'avait pas prévues Einstein pour expliquer l'anomalie de Mercure, et la déviation de la lumière. C'est bien, mais on ne saurait oublier que la première de ces formules exactes, celle d'Einstein, a audacieusement précédé la vérification.

Dans la bataille contre l'éternel ennemi, l'Inconnu, des tranchées nouvelles ont été conquises. Certes, il importe de les organiser et de creuser des cheminements qui y accèdent plus directement. Mais il faudra demain marcher encore de l'avant, gagner encore du terrain. Il faudra, par quelque détour théorique que ce soit, annoncer d'autres faits nouveaux, imprévus et vérifiables. C'est ainsi qu'a fait Einstein.

Si c'est une faiblesse pour la doctrine einsteinienne de dénier toute objectivité, tout privilège à l'un quelconque des systèmes de référence... tout en utilisant un tel système pour les besoins du calcul, cette faiblesse du moins aurait été aussi celle d'Henri Poincaré.

Jusqu'à sa mort il s'est insurgé vigoureusement contre la conception newtonienne. L'adhésion de ce puissant esprit qu'on retrouve à tous les carrefours [215] des découvertes modernes, suffirait à assurer le respect à la doctrine relativiste.

D'un côté s'il y a Newton, devant qui se dresse maintenant un défenseur ardent et persuasif, armé d'un vif génie mathématique, Paul Painlevé, de l'autre il y a Einstein et près de lui Henri Poincaré. Déjà l'histoire de part et d'autre de la même barricade nous avait montré Aristote contre Épicure, Copernic contre les scholastiques.

Bataille éternelle d'idées qui est peut-être sans issue, si, comme le croyait Poincaré, le principe de relativité n'est au fond qu'une convention que l'expérience ne peut prendre en défaut parce que, appliquée à l'Univers entier, elle est invérifiable.

Ce qui prouve que la doctrine einsteinienne est forte et vraie, c'est qu'elle est féconde. Les êtres nouveaux dont elle a peuplé la science, et qui sont les découvertes amenées et prédites par elle, sont-ils des enfants légitimes? Les newtoniens disent que non. Mais dans une science bien faite comme dans un état idéal, ce qui importe ce sont les enfants, ce n'est pas leur légitimité.

Du moins la vigoureuse contre-offensive de M. Paul Painlevé aura ramené dans leurs lignes les zélateurs trop pressés de l'évangile nouveau, qui déjà pensaient avoir pulvérisé, sans espoir de revanche, toute la science classique.

Chacun reste maintenant sur ses positions, et il n'est plus question de considérer comme un enfantillage barbare la conception newtonienne du monde.

[216] En face une autre conception se dresse et voilà tout. Entre elles la bataille est indécise et peut-être le sera toujours, les armes capables de déclencher la victoire devant rester à jamais scellées dans l'arsenal métaphysique.

Quoi qu'il advienne, la doctrine d'Einstein possède une puissance de synthèse et de prévision qui nécessairement fondra son majestueux ensemble d'équations dans la science de demain.

M. Émile Picard, secrétaire perpétuel de l'Académie des Sciences, qui est un des esprits lumineux et profonds de ce temps, s'est demandé si c'est un progrès de «chercher à ramener, comme l'a fait Einstein, la Physique à la Géométrie».

Sans nous attarder à cette question qui est peut-être insoluble, comme toutes les questions spéculatives, nous conclurons avec l'illustre mathématicien que seuls importent l'accord des formules finales avec les faits et le moule analytique où la théorie enferme les phénomènes.

Considérée sous cet angle, la théorie d'Einstein a la solidité de l'airain. Son exactitude consiste dans sa force explicative et dans les découvertes expérimentales prédites par elle et aussitôt réalisées.

Ce qui change dans les théories ce sont les images qu'on se crée des objets entre lesquels la science [217] découvre et établit des rapports. Parfois on remplace ces images, mais les rapports restent vrais s'ils reposent sur des faits bien observés.

Grâce à ce fonds commun de vérité, les théories les plus éphémères ne meurent pas tout entières. Elles se transmettent, comme le flambeau des coureurs antiques, la seule réalité accessible: les lois qui expriment les rapports des choses.

Il arrive aujourd'hui que deux théories tiennent ensemble dans leurs mains jointes le flambeau sacré. La vision einsteinienne et la vision newtonienne du monde en sont deux reflets véridiques. Ainsi les deux images polarisées en sens contraire, que le spath d'Islande nous montre à travers son étrange cristal, participent toutes deux de la lumière du même objet.

Tragiquement isolé, prisonnier de son «moi», l'homme a fait un effort désespéré pour «sauter par-dessus son ombre», pour étreindre le monde extérieur. De cet effort a jailli la Science dont les antennes merveilleuses prolongent subtilement nos sensations. Ainsi nous avons approché par endroits les brillantes parures de la réalité. Mais, à côté du mystère rémanent, les choses qu'on sait sont aussi petites que les étoiles du Ciel par rapport à l'abîme où elles flottent.

Einstein au fond de l'inconnu nous a dévoilé des clartés nouvelles.

Il est, et restera un des phares de la pensée humaine.

IMPRIMERIE
PAUL BRODARD
COULOMMIERS

End of Project Gutenberg's Einstein et l'univers, by Charles Nordmann

*** END OF THIS PROJECT GUTENBERG EBOOK EINSTEIN ET L'UNIVERS ***

***** This file should be named 41903-h.htm or 41903-h.zip *****
This and all associated files of various formats will be found in:
        http://www.gutenberg.org/4/1/9/0/41903/

Produced by Claudine Corbasson, Hans Pieterse and the
Online Distributed Proofreading Team at http://www.pgdp.net
(This file was produced from images generously made
available by The Internet Archive/Canadian Libraries)


Updated editions will replace the previous one--the old editions
will be renamed.

Creating the works from public domain print editions means that no
one owns a United States copyright in these works, so the Foundation
(and you!) can copy and distribute it in the United States without
permission and without paying copyright royalties.  Special rules,
set forth in the General Terms of Use part of this license, apply to
copying and distributing Project Gutenberg-tm electronic works to
protect the PROJECT GUTENBERG-tm concept and trademark.  Project
Gutenberg is a registered trademark, and may not be used if you
charge for the eBooks, unless you receive specific permission.  If you
do not charge anything for copies of this eBook, complying with the
rules is very easy.  You may use this eBook for nearly any purpose
such as creation of derivative works, reports, performances and
research.  They may be modified and printed and given away--you may do
practically ANYTHING with public domain eBooks.  Redistribution is
subject to the trademark license, especially commercial
redistribution.



*** START: FULL LICENSE ***

THE FULL PROJECT GUTENBERG LICENSE
PLEASE READ THIS BEFORE YOU DISTRIBUTE OR USE THIS WORK

To protect the Project Gutenberg-tm mission of promoting the free
distribution of electronic works, by using or distributing this work
(or any other work associated in any way with the phrase "Project
Gutenberg"), you agree to comply with all the terms of the Full Project
Gutenberg-tm License available with this file or online at
  www.gutenberg.org/license.


Section 1.  General Terms of Use and Redistributing Project Gutenberg-tm
electronic works

1.A.  By reading or using any part of this Project Gutenberg-tm
electronic work, you indicate that you have read, understand, agree to
and accept all the terms of this license and intellectual property
(trademark/copyright) agreement.  If you do not agree to abide by all
the terms of this agreement, you must cease using and return or destroy
all copies of Project Gutenberg-tm electronic works in your possession.
If you paid a fee for obtaining a copy of or access to a Project
Gutenberg-tm electronic work and you do not agree to be bound by the
terms of this agreement, you may obtain a refund from the person or
entity to whom you paid the fee as set forth in paragraph 1.E.8.

1.B.  "Project Gutenberg" is a registered trademark.  It may only be
used on or associated in any way with an electronic work by people who
agree to be bound by the terms of this agreement.  There are a few
things that you can do with most Project Gutenberg-tm electronic works
even without complying with the full terms of this agreement.  See
paragraph 1.C below.  There are a lot of things you can do with Project
Gutenberg-tm electronic works if you follow the terms of this agreement
and help preserve free future access to Project Gutenberg-tm electronic
works.  See paragraph 1.E below.

1.C.  The Project Gutenberg Literary Archive Foundation ("the Foundation"
or PGLAF), owns a compilation copyright in the collection of Project
Gutenberg-tm electronic works.  Nearly all the individual works in the
collection are in the public domain in the United States.  If an
individual work is in the public domain in the United States and you are
located in the United States, we do not claim a right to prevent you from
copying, distributing, performing, displaying or creating derivative
works based on the work as long as all references to Project Gutenberg
are removed.  Of course, we hope that you will support the Project
Gutenberg-tm mission of promoting free access to electronic works by
freely sharing Project Gutenberg-tm works in compliance with the terms of
this agreement for keeping the Project Gutenberg-tm name associated with
the work.  You can easily comply with the terms of this agreement by
keeping this work in the same format with its attached full Project
Gutenberg-tm License when you share it without charge with others.

1.D.  The copyright laws of the place where you are located also govern
what you can do with this work.  Copyright laws in most countries are in
a constant state of change.  If you are outside the United States, check
the laws of your country in addition to the terms of this agreement
before downloading, copying, displaying, performing, distributing or
creating derivative works based on this work or any other Project
Gutenberg-tm work.  The Foundation makes no representations concerning
the copyright status of any work in any country outside the United
States.

1.E.  Unless you have removed all references to Project Gutenberg:

1.E.1.  The following sentence, with active links to, or other immediate
access to, the full Project Gutenberg-tm License must appear prominently
whenever any copy of a Project Gutenberg-tm work (any work on which the
phrase "Project Gutenberg" appears, or with which the phrase "Project
Gutenberg" is associated) is accessed, displayed, performed, viewed,
copied or distributed:

This eBook is for the use of anyone anywhere at no cost and with
almost no restrictions whatsoever.  You may copy it, give it away or
re-use it under the terms of the Project Gutenberg License included
with this eBook or online at www.gutenberg.org

1.E.2.  If an individual Project Gutenberg-tm electronic work is derived
from the public domain (does not contain a notice indicating that it is
posted with permission of the copyright holder), the work can be copied
and distributed to anyone in the United States without paying any fees
or charges.  If you are redistributing or providing access to a work
with the phrase "Project Gutenberg" associated with or appearing on the
work, you must comply either with the requirements of paragraphs 1.E.1
through 1.E.7 or obtain permission for the use of the work and the
Project Gutenberg-tm trademark as set forth in paragraphs 1.E.8 or
1.E.9.

1.E.3.  If an individual Project Gutenberg-tm electronic work is posted
with the permission of the copyright holder, your use and distribution
must comply with both paragraphs 1.E.1 through 1.E.7 and any additional
terms imposed by the copyright holder.  Additional terms will be linked
to the Project Gutenberg-tm License for all works posted with the
permission of the copyright holder found at the beginning of this work.

1.E.4.  Do not unlink or detach or remove the full Project Gutenberg-tm
License terms from this work, or any files containing a part of this
work or any other work associated with Project Gutenberg-tm.

1.E.5.  Do not copy, display, perform, distribute or redistribute this
electronic work, or any part of this electronic work, without
prominently displaying the sentence set forth in paragraph 1.E.1 with
active links or immediate access to the full terms of the Project
Gutenberg-tm License.

1.E.6.  You may convert to and distribute this work in any binary,
compressed, marked up, nonproprietary or proprietary form, including any
word processing or hypertext form.  However, if you provide access to or
distribute copies of a Project Gutenberg-tm work in a format other than
"Plain Vanilla ASCII" or other format used in the official version
posted on the official Project Gutenberg-tm web site (www.gutenberg.org),
you must, at no additional cost, fee or expense to the user, provide a
copy, a means of exporting a copy, or a means of obtaining a copy upon
request, of the work in its original "Plain Vanilla ASCII" or other
form.  Any alternate format must include the full Project Gutenberg-tm
License as specified in paragraph 1.E.1.

1.E.7.  Do not charge a fee for access to, viewing, displaying,
performing, copying or distributing any Project Gutenberg-tm works
unless you comply with paragraph 1.E.8 or 1.E.9.

1.E.8.  You may charge a reasonable fee for copies of or providing
access to or distributing Project Gutenberg-tm electronic works provided
that

- You pay a royalty fee of 20% of the gross profits you derive from
     the use of Project Gutenberg-tm works calculated using the method
     you already use to calculate your applicable taxes.  The fee is
     owed to the owner of the Project Gutenberg-tm trademark, but he
     has agreed to donate royalties under this paragraph to the
     Project Gutenberg Literary Archive Foundation.  Royalty payments
     must be paid within 60 days following each date on which you
     prepare (or are legally required to prepare) your periodic tax
     returns.  Royalty payments should be clearly marked as such and
     sent to the Project Gutenberg Literary Archive Foundation at the
     address specified in Section 4, "Information about donations to
     the Project Gutenberg Literary Archive Foundation."

- You provide a full refund of any money paid by a user who notifies
     you in writing (or by e-mail) within 30 days of receipt that s/he
     does not agree to the terms of the full Project Gutenberg-tm
     License.  You must require such a user to return or
     destroy all copies of the works possessed in a physical medium
     and discontinue all use of and all access to other copies of
     Project Gutenberg-tm works.

- You provide, in accordance with paragraph 1.F.3, a full refund of any
     money paid for a work or a replacement copy, if a defect in the
     electronic work is discovered and reported to you within 90 days
     of receipt of the work.

- You comply with all other terms of this agreement for free
     distribution of Project Gutenberg-tm works.

1.E.9.  If you wish to charge a fee or distribute a Project Gutenberg-tm
electronic work or group of works on different terms than are set
forth in this agreement, you must obtain permission in writing from
both the Project Gutenberg Literary Archive Foundation and Michael
Hart, the owner of the Project Gutenberg-tm trademark.  Contact the
Foundation as set forth in Section 3 below.

1.F.

1.F.1.  Project Gutenberg volunteers and employees expend considerable
effort to identify, do copyright research on, transcribe and proofread
public domain works in creating the Project Gutenberg-tm
collection.  Despite these efforts, Project Gutenberg-tm electronic
works, and the medium on which they may be stored, may contain
"Defects," such as, but not limited to, incomplete, inaccurate or
corrupt data, transcription errors, a copyright or other intellectual
property infringement, a defective or damaged disk or other medium, a
computer virus, or computer codes that damage or cannot be read by
your equipment.

1.F.2.  LIMITED WARRANTY, DISCLAIMER OF DAMAGES - Except for the "Right
of Replacement or Refund" described in paragraph 1.F.3, the Project
Gutenberg Literary Archive Foundation, the owner of the Project
Gutenberg-tm trademark, and any other party distributing a Project
Gutenberg-tm electronic work under this agreement, disclaim all
liability to you for damages, costs and expenses, including legal
fees.  YOU AGREE THAT YOU HAVE NO REMEDIES FOR NEGLIGENCE, STRICT
LIABILITY, BREACH OF WARRANTY OR BREACH OF CONTRACT EXCEPT THOSE
PROVIDED IN PARAGRAPH 1.F.3.  YOU AGREE THAT THE FOUNDATION, THE
TRADEMARK OWNER, AND ANY DISTRIBUTOR UNDER THIS AGREEMENT WILL NOT BE
LIABLE TO YOU FOR ACTUAL, DIRECT, INDIRECT, CONSEQUENTIAL, PUNITIVE OR
INCIDENTAL DAMAGES EVEN IF YOU GIVE NOTICE OF THE POSSIBILITY OF SUCH
DAMAGE.

1.F.3.  LIMITED RIGHT OF REPLACEMENT OR REFUND - If you discover a
defect in this electronic work within 90 days of receiving it, you can
receive a refund of the money (if any) you paid for it by sending a
written explanation to the person you received the work from.  If you
received the work on a physical medium, you must return the medium with
your written explanation.  The person or entity that provided you with
the defective work may elect to provide a replacement copy in lieu of a
refund.  If you received the work electronically, the person or entity
providing it to you may choose to give you a second opportunity to
receive the work electronically in lieu of a refund.  If the second copy
is also defective, you may demand a refund in writing without further
opportunities to fix the problem.

1.F.4.  Except for the limited right of replacement or refund set forth
in paragraph 1.F.3, this work is provided to you 'AS-IS', WITH NO OTHER
WARRANTIES OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO
WARRANTIES OF MERCHANTABILITY OR FITNESS FOR ANY PURPOSE.

1.F.5.  Some states do not allow disclaimers of certain implied
warranties or the exclusion or limitation of certain types of damages.
If any disclaimer or limitation set forth in this agreement violates the
law of the state applicable to this agreement, the agreement shall be
interpreted to make the maximum disclaimer or limitation permitted by
the applicable state law.  The invalidity or unenforceability of any
provision of this agreement shall not void the remaining provisions.

1.F.6.  INDEMNITY - You agree to indemnify and hold the Foundation, the
trademark owner, any agent or employee of the Foundation, anyone
providing copies of Project Gutenberg-tm electronic works in accordance
with this agreement, and any volunteers associated with the production,
promotion and distribution of Project Gutenberg-tm electronic works,
harmless from all liability, costs and expenses, including legal fees,
that arise directly or indirectly from any of the following which you do
or cause to occur: (a) distribution of this or any Project Gutenberg-tm
work, (b) alteration, modification, or additions or deletions to any
Project Gutenberg-tm work, and (c) any Defect you cause.


Section  2.  Information about the Mission of Project Gutenberg-tm

Project Gutenberg-tm is synonymous with the free distribution of
electronic works in formats readable by the widest variety of computers
including obsolete, old, middle-aged and new computers.  It exists
because of the efforts of hundreds of volunteers and donations from
people in all walks of life.

Volunteers and financial support to provide volunteers with the
assistance they need are critical to reaching Project Gutenberg-tm's
goals and ensuring that the Project Gutenberg-tm collection will
remain freely available for generations to come.  In 2001, the Project
Gutenberg Literary Archive Foundation was created to provide a secure
and permanent future for Project Gutenberg-tm and future generations.
To learn more about the Project Gutenberg Literary Archive Foundation
and how your efforts and donations can help, see Sections 3 and 4
and the Foundation information page at www.gutenberg.org


Section 3.  Information about the Project Gutenberg Literary Archive
Foundation

The Project Gutenberg Literary Archive Foundation is a non profit
501(c)(3) educational corporation organized under the laws of the
state of Mississippi and granted tax exempt status by the Internal
Revenue Service.  The Foundation's EIN or federal tax identification
number is 64-6221541.  Contributions to the Project Gutenberg
Literary Archive Foundation are tax deductible to the full extent
permitted by U.S. federal laws and your state's laws.

The Foundation's principal office is located at 4557 Melan Dr. S.
Fairbanks, AK, 99712., but its volunteers and employees are scattered
throughout numerous locations.  Its business office is located at 809
North 1500 West, Salt Lake City, UT 84116, (801) 596-1887.  Email
contact links and up to date contact information can be found at the
Foundation's web site and official page at www.gutenberg.org/contact

For additional contact information:
     Dr. Gregory B. Newby
     Chief Executive and Director
     gbnewby@pglaf.org

Section 4.  Information about Donations to the Project Gutenberg
Literary Archive Foundation

Project Gutenberg-tm depends upon and cannot survive without wide
spread public support and donations to carry out its mission of
increasing the number of public domain and licensed works that can be
freely distributed in machine readable form accessible by the widest
array of equipment including outdated equipment.  Many small donations
($1 to $5,000) are particularly important to maintaining tax exempt
status with the IRS.

The Foundation is committed to complying with the laws regulating
charities and charitable donations in all 50 states of the United
States.  Compliance requirements are not uniform and it takes a
considerable effort, much paperwork and many fees to meet and keep up
with these requirements.  We do not solicit donations in locations
where we have not received written confirmation of compliance.  To
SEND DONATIONS or determine the status of compliance for any
particular state visit www.gutenberg.org/donate

While we cannot and do not solicit contributions from states where we
have not met the solicitation requirements, we know of no prohibition
against accepting unsolicited donations from donors in such states who
approach us with offers to donate.

International donations are gratefully accepted, but we cannot make
any statements concerning tax treatment of donations received from
outside the United States.  U.S. laws alone swamp our small staff.

Please check the Project Gutenberg Web pages for current donation
methods and addresses.  Donations are accepted in a number of other
ways including checks, online payments and credit card donations.
To donate, please visit:  www.gutenberg.org/donate


Section 5.  General Information About Project Gutenberg-tm electronic
works.

Professor Michael S. Hart was the originator of the Project Gutenberg-tm
concept of a library of electronic works that could be freely shared
with anyone.  For forty years, he produced and distributed Project
Gutenberg-tm eBooks with only a loose network of volunteer support.

Project Gutenberg-tm eBooks are often created from several printed
editions, all of which are confirmed as Public Domain in the U.S.
unless a copyright notice is included.  Thus, we do not necessarily
keep eBooks in compliance with any particular paper edition.

Most people start at our Web site which has the main PG search facility:

     www.gutenberg.org

This Web site includes information about Project Gutenberg-tm,
including how to make donations to the Project Gutenberg Literary
Archive Foundation, how to help produce our new eBooks, and how to
subscribe to our email newsletter to hear about new eBooks.